ASIC，大救星！_風聞

不斷增長的人工智能（AI）需求暴露出一個嚴峻的“計算危機”，其特點是能源消耗不可持續、訓練成本過高以及傳統互補式金屬氧化物半導體（CMOS）微縮技術接近極限。「基於物理的專用集成電路（ASIC）」提供了一種變革性的範式，它直接利用固有的物理動力學進行計算，而不是耗費資源來強制實現理想化的數字抽象。

通過放寬傳統ASIC所需的約束，例如強制無狀態性、單向性、確定性和同步性，這些設備旨在作為物理過程的精確實現而運行，從而在能源效率和計算吞吐量方面獲得顯著提升。這種方法能夠實現新穎的協同設計策略，使算法需求與物理系統固有的計算原語相吻合。

基於物理的ASIC可以加速關鍵的AI應用，例如擴散模型、採樣、優化和神經網絡推理，以及材料和分子科學模擬等傳統計算負載。最終，這一願景指向了一個異構、高度專業化的計算平台未來，它能夠克服當前的擴展瓶頸，並開啓計算能力和效率的新前沿。

一、引言：計算危機

在過去十年中，人工智能（AI）應用的快速擴展顯著增加了對計算基礎設施的需求，暴露了基礎硬件範式中的關鍵限制。支撐AI模型的基礎設施從未考慮到今天的規模、複雜性或能源需求。因此，當前的計算堆棧導致了當前硬件系統中固有的物理計算能力的嚴重低效利用。

傳統的擴展正面臨多方面的極限：

1.AI的能源需求正在不可持續地增加，如圖1(a)所示。數據中心是AI操作的核心，2023年消耗了大約200太瓦時（TWh）的電力。預測表明，到2026年，這一數字可能會增至260太瓦時，佔美國總電力需求的約6%。

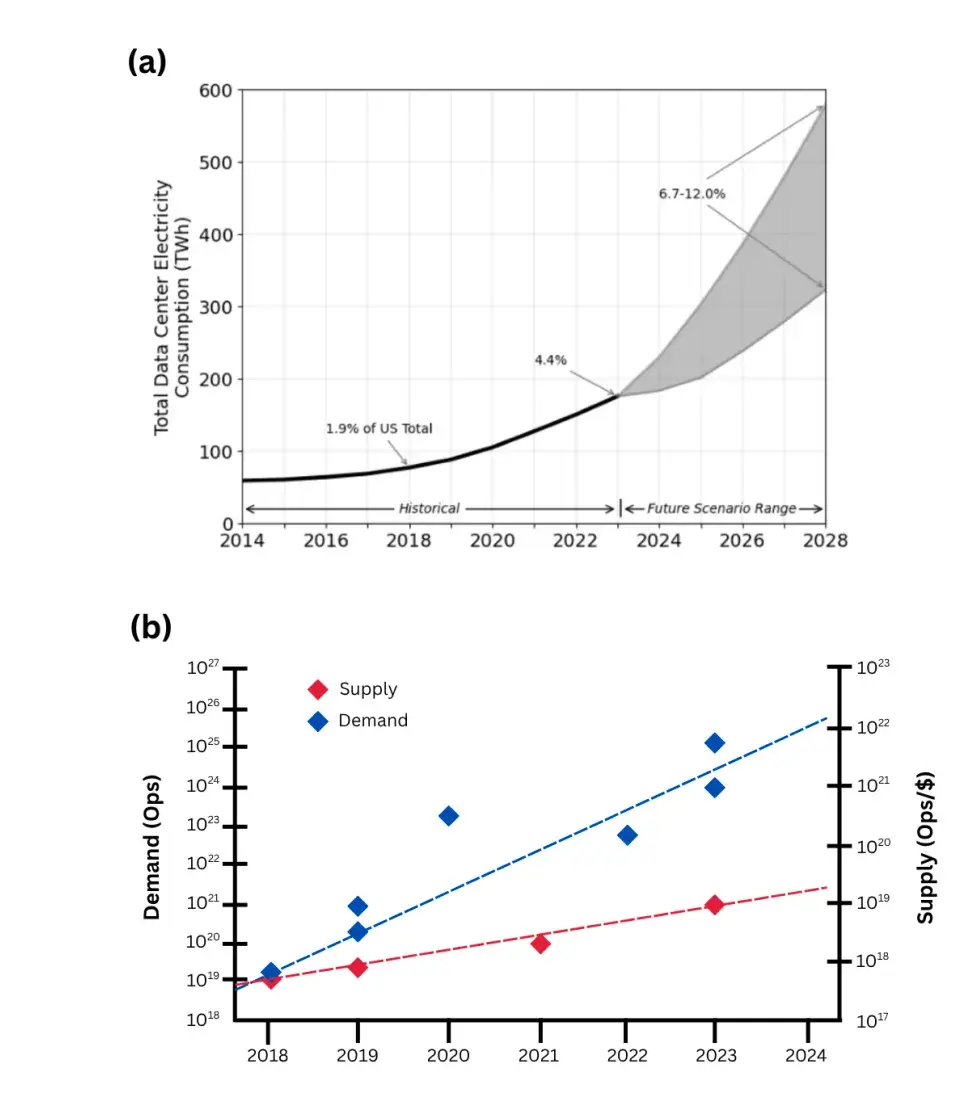圖 1. 預計的計算能耗與計算能力供需情況。雖然“計算危機”有多重面向，但兩個關鍵方面是：（a）計算能耗的不斷上升；（b）計算能力供需差距的不斷擴大（此處以 AI 模型訓練為例）。過去幾年中，這兩個問題在很大程度上都是由 AI 革命所驅動的。圖中（a）和（b）分別改編自參考文獻 [3] 和 [4]。

2. 計算成本急劇上升，集中化了訪問。前沿AI模型的發展使得訓練成本大幅增加，預計到2027年，最大規模的訓練運行成本將超過10億美元。這與圖1(b)所示的供需差距自然相關。

3. 隨着晶體管尺寸縮小到納米級，長期以來的擴展定律——摩爾定律和丹納德定律——正在達到其極限。諸如隨機性、漏電流和可變性等微型化效應使得在這些尺度下實現可靠操作變得困難。我們無法再像過去那樣按比例減少閾值電壓，從而導致更高的功率密度，進而導致加熱，限制了時鐘速度和運行時間。

這些限制不僅妨礙了性能的提升，還揭示了更深層次的低效：今天的通用架構未能充分利用硬件本身的物理潛力。為管理複雜性而設計的抽象層如今成為了瓶頸，尤其是在能源效率和計算吞吐量方面。如果不改變計算範式，我們面臨創新停滯、能源成本上升，並且AI能力可能集中在少數大型公司和政府機構手中的風險。

基於物理的應用特定集成電路（ASIC）通過利用物理現象進行計算，而非壓制它們，提供了一種變革性的方法。通過將硬件設計與物理系統的內在屬性對齊，這些ASIC可以提高效率、降低能耗，並使AI和計算資源的獲取更加普及。

二、什麼是基於物理的ASIC？

A. 動機

如果我們想提高計算效率（例如，減少能耗或縮短時間），我們可以為理想化的通用硬件設計更高效的算法，創建更快或更高效的硬件（無論是通用的還是專用的），或者聯合設計算法和硬件，旨在最大化所獲得的有效計算。雖然在當代計算機科學和工程的研究領域中有許多例外，但在過去五十年左右，明確致力於改善計算的努力主要集中在前兩條途徑上，即通用計算硬件和高度抽象的軟件開發策略，這種策略使得不斷擴展的軟件應用和現代數字經濟得以實現。

然而，更多專用硬件，如GPU，仍然成為計算領域最近進展的關鍵推動力，硬件的隱性算法偏好長期以來一直是算法成功的指導力量。

機器學習中最流行的算法恰好主要涉及矩陣乘法運算，而GPU在這一操作上特別高效，這難道是巧合嗎？當然不是：這些算法在軟件與硬件之間實現了出色的匹配，使得它們能夠很好地擴展，取得比那些未能有效利用GPU的算法更好的結果。這種普遍趨勢，即算法的共同優化在無意識中受到現有硬件特性引導，被稱為“硬件彩票[5]”。硬件彩票的突出性表明，軟件和硬件的協同設計是不可避免的，無論是有意識的還是無意識的。

基於物理的ASIC的思想本質上是將這一主要無意的趨勢轉變為完全有意且有原則的做法：它旨在故意將算法和硬件從可用、可擴展的硬件基礎設施的最低物理層面開始進行協同設計。類似於變換器（Transformers）中密集的矩陣乘法巧妙地適應了GPU的偏好，我們是否可以類似地設計算法和電子芯片，利用硅電子電路物理學中更深層的偏好（進而解鎖更大的可擴展性）？

當然，這不是免費的午餐：它將需要開發新的算法和硬件，而這些算法和硬件與大多數現代計算機科學家設計的不同，必須考慮到彼此的細節。但另一方面，這條道路可能使我們能夠比今天更高效地利用現代計算硬件。效率能提高多少？這很難説，但我們可以通過考慮一個相關問題來得到一些線索，即抽象如何影響數字模擬電路的成本。例如，執行簡單CMOS非門的物理設備在被抽象為二進制邏輯門時，每個時鐘週期執行一個二進制操作，但如果我們改為模擬組成它的電路的瞬態（和模擬）動態，典型的數值方法（例如，在SPICE中使用的）可能需要數百萬次浮動點操作。如果我們將每個晶體管細緻地建模（正如在設計階段經常做的那樣），我們必然要解決3+1維的偏微分方程系統，要求數十億甚至數萬億次浮動點操作（僅僅對於一個時鐘週期）。顯然，我們抽象一個物理系統的物理層次可能會影響它等價於多少次數字邏輯門操作。然而，這只是挑戰的一部分：僅僅因為在某個抽象層次上對物理系統的模擬是昂貴的，並不一定意味着我們可以使用相同的物理系統和抽象來執行其他有趣的計算。這就是基於物理的ASIC的核心挑戰：設計抽象、算法和硬件架構，通過更好地尊重基礎硬件的物理規律，使我們能夠有效地、更加充分地利用今天高度可擴展的電子電路所提供的物理計算能力。

B. 定義

寬泛地説，基於物理的ASIC是依賴於系統自然物理動態來執行數據上的非平凡操作的ASIC。這個定義有些模糊；因為所有電路都是遵循物理定律的，所以所有計算在某種意義上都是通過計算系統的自然演化來完成的。

然而，傳統的ASIC設計有意壓制或抽象掉某些物理效應，以實現理想化的、符號化的計算模型。通過這樣做，它依賴於一組近似，這些近似允許從簡單、理想化的組件中構建複雜系統。

最重要的近似之一是：

1. 無狀態性：在傳統的ASIC中，通常存在一個明確的分離，即內存和計算由不同位置的獨立組件處理。不負責存儲信息的組件被假定為其輸出僅依賴於當前輸入，而不依賴於先前的歷史。例如，一個NOT門應該反轉其輸入的當前值，而不管過去的值如何。

2. 單向性：傳統ASIC的基本組件被設計成在單一方向上傳播信息；它們有指定的輸入和輸出端口。例如，一個NOT門應該響應輸入端的變化，但它的輸出不應該影響輸入。正因為如此，在傳統的ASIC中創建反饋迴路需要顯式地將某個模塊的輸出連接到其輸入。

3. 決定性：在相同的輸入和初始條件下，電路預期每次都產生相同的輸出。

4. 同步：通常，傳統ASIC中不同部分的信號是根據一個集中的時鐘相互同步的。

這些屬性在嚴格意義上是無法在物理上實現的：實際組件會表現出記憶效應、反饋、噪聲和熱波動。強制實現這些理想行為會帶來能量、延遲或複雜性的成本，並且隨着近似的精確度提高，這些成本也會增加。

基於物理的ASIC則被設計為在不依賴這些屬性（或至少不依賴其中某些屬性）的情況下運作。與傳統ASIC不同，這些設備被設計成利用（或至少容忍）有狀態性、雙向性、非決定性和異步性，如圖2所示。因此，基於物理的ASIC上的計算不是對非物理過程的近似，而是物理過程的實現。

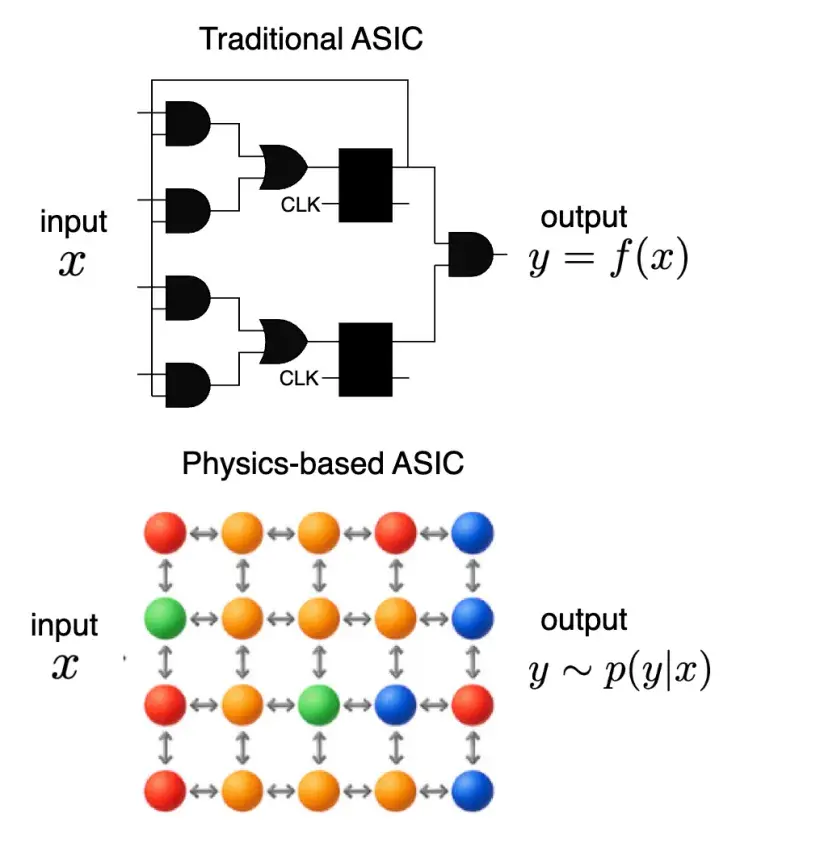圖 2. 傳統ASIC 與基於物理的ASIC。 如圖所示，傳統ASIC將存儲與計算分離，假定計算組件是無狀態的。單個邏輯門以單向方式傳遞信息，具有專用的輸入和輸出端，要構建反饋迴路必須顯式地將輸出接回輸入。基於物理的ASIC則可能包含有狀態的計算組件，並且在耦合之間具有雙向的信息流動。

由於缺乏傳統ASIC中存在的簡化假設，基於物理的ASIC的行為通常更加複雜，且更難以分析。然而，基於物理的ASIC中的電路組件執行操作時也有更廣泛的可能性。因此，基於物理的ASIC通常能夠用更少的組件完成顯著更多的計算。例如，傳統ASIC中的標量乘法可能需要幾十到幾百個晶體管，而在基於物理的ASIC中只需要少量組件。

C. 平台

許多現有的非常規計算範式可以看作是基於物理的ASIC的例子。儘管這些不同方法之間存在很大多樣性，但基於物理的ASIC與其他基於物理的平台（例如，用肥皂泡進行計算[6]）的區別在於它們的可擴展性。可擴展性和可製造性是這個激動人心的新領域的關鍵要素。現在我們給出這些可擴展平台的一些例子，其中一些已在圖3中示出。

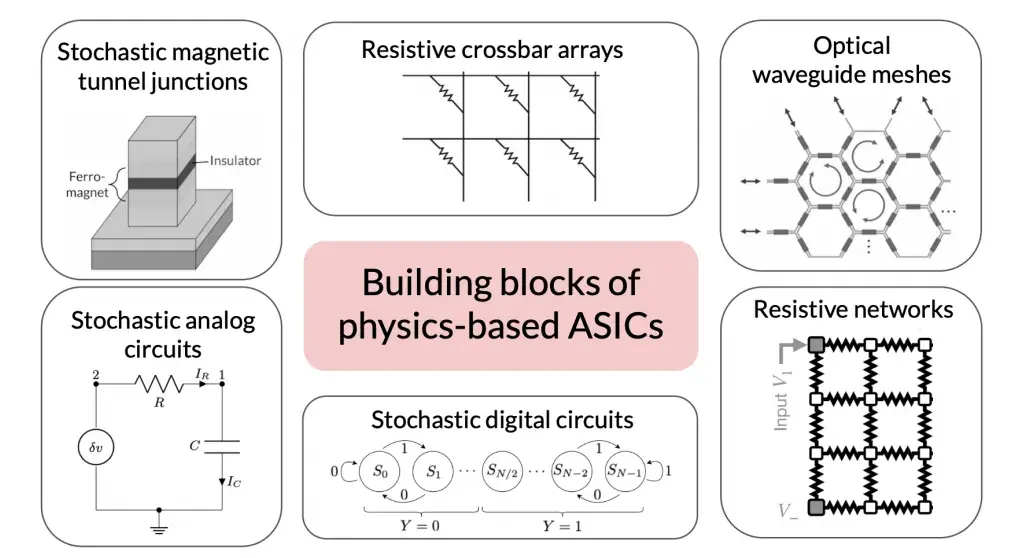圖 3. 基於物理的ASIC的常見構建模塊。 雖然並非詳盡無遺，但圖中展示了幾種可用作基於物理的ASIC構建模塊的基本物理結構。對於每一種組件，其所遵循的物理定律都可映射為某種計算原語操作。

如前所述，基於物理的ASIC與傳統ASIC的不同之處在於它們放寬了通常應當大致滿足的某些要求，包括無狀態性、單向性、決定性和同步性。在基於物理的ASIC中，我們可以大致根據這些要求的子集來對設備進行分類。

已經提出了一些範式，其中ASIC中的電路組件故意被設計為有狀態的，有時依賴於較長時間內的歷史。例如，使用憶阻器的電路就是一個典型的例子，其電阻依賴於通過它們的電荷量。其他組件在用於模擬電路時也可能表現出記憶效應，從而去除了無狀態性的假設。

雙向耦合在實現Ising機（包括數字和模擬）的ASIC中很常見，在設計用來解決線性和非線性代數及（可能是隨機的）微分方程問題的模擬設備中也是如此。物理自由度之間的相互作用也被用於基於非線性光子學的平台和自調整電阻網絡。

由於抑制有狀態行為和雙向信息流需要耗散，我們可以預期，當這些要求被放寬時，可能會實現更高的能效。如果把這個想法推向極致，可逆計算試圖通過避免任何信息擦除來顯著減少能量損耗。值得注意的是，量子計算作為可逆計算的一個子集，表現出交互的量子比特之間的信息雙向流動。

近年來，對非決定性ASIC（包括模擬和數字）的興趣也在不斷增長。在數字情況下，已有大量關於p比特的研究，這些比特是經歷連續時間馬爾可夫過程（CTMC）的二進制變量。磁隧道結（MTJ）在電壓中表現出雙穩態的隨機行為，可用作模擬或數字隨機性的來源。類似地，熱力學計算機使用模擬電路採用連續變量的隨機動力學（即布朗運動）。

在一些基於物理的ASIC技術中，包括p比特，採用了無中央時鐘的設計，單個設備中的不同信號將異步變化。也有一些ASIC利用多同步時鐘設計，其中並非使用單一的中央時鐘，而是多個本地時鐘，這些時鐘之間並不完全同步。

D. 性能優勢的直覺

如前所述，傳統的ASIC會產生與確保無狀態性、單向性、決定性和同步性要求大致滿足相關的時間和能量成本。一般來説，這些成本通常是值得的，因為它們允許計算系統以非常模塊化的方式設計，可以用於各種用途。然而，對於特定類型的問題，通常存在一些算法或解決方法，這些方法不依賴於這些屬性。在這種情況下，設計一個ASIC來解決該特定類型的問題，並放寬與確保無狀態性、單向性和/或決定性相關的設計約束，可能會更為有利。

從實際角度來看，這可能表現為提高時鐘頻率，超過了可以依賴無狀態或決定性行為的範圍。同樣，降低供電電壓，也會產生非決定性行為，以換取更低的功耗。事實上，基於物理的ASIC的一個常見特點是，它們通常通過放寬上述約束來節省功率和能量成本。

有趣的是，我們還常常觀察到，當系統的自然動態在計算中被利用時，許多操作可以融合成一個操作。也就是説，我們可以看到，在某種意義上，物理動態“自動”地執行部分計算（例如，求解線性代數或優化問題）。這為時間和能量節省的可能來源提供了一些直覺。

儘管在將各種基於物理的ASIC方法進行擴展方面仍然有很多工作要做，但已有跡象表明，在時間和能量成本上存在顯著優勢的潛力。

三、設計策略

A. 自上而下 vs. 自下而上

設計基於物理的ASIC是具有挑戰性的。一種有原則的策略通常涉及考慮自上而下與自下而上視角之間的交集，如圖4所示。在自上而下的方法中，從一個具有廣泛興趣或重大影響的關鍵應用A開始（例如，圖像或材料的生成AI）。然後將這個應用映射到算法空間，即列出一組可能運行該應用的算法L(A)（例如，擴散模型、變換器等）。

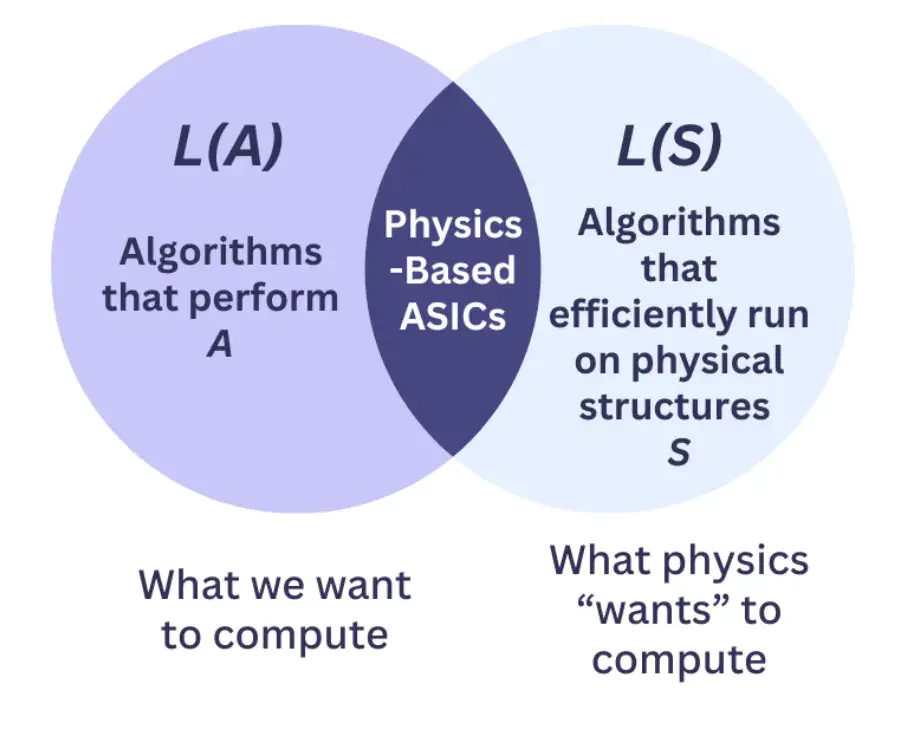圖 4. 基於物理的ASIC設計。 自上而下方法給出可運行目標應用 A 的一組算法 L(A)。自下而上方法給出可在某種物理結構 S 上高效運行的一組算法 L(S)。基本設計原則是最大化這兩組算法之間的重疊。

或者，在自下而上的方法中，從基本的物理結構S開始，如圖3中展示的某個結構。然後確定可以使用這些結構高效計算的數學原語P(S)。接着，從這些原語中形成算法，找到可以高效運行的算法集合L(S)。目標是最大化L(A)和L(S)這兩個集合之間的重疊。通常，這需要考慮多個不同的候選結構S，然後選擇那個在算法空間中與目標應用A最佳匹配的結構。

不同領域可能會從這種策略中受益。例如，在量子計算中，通常採用自下而上的視角，專注於物理結構（例如離子、原子、超導電路等）。同時，將量子計算視為基於物理的ASIC的特例也是合理的。因此，在量子背景下使用上述框架可能是設計量子ASIC的一種有用視角，前提是要牢記希望與目標應用A相交的算法集合L(A)。

B. 性能指標

我們可以通過使策略更具量化性來完善這一策略。即，我們必須澄清算法在某些硬件上“高效”運行意味着什麼。雖然有多種潛在的性能指標，但兩個關鍵指標是運行時間和能量消耗。對於給定的算法ℓ，確定ℓ是否屬於L(S)可以通過比較ℓ在兩種硬件上的運行時間和能量消耗來實現：最先進的（SOTA）數字硬件（通常是GPU）和由結構S構建的硬件。

為此，我們定義了以下比率：

將算法ℓ納入集合L(S)的合理標準是，RT(ℓ)或RE(ℓ)中的任意一個大於1。另一方面，如果這兩個比率都小於1，則算法ℓ不被認為在硬件S上高效。

需要考慮的一個警告是，時間和能量可以相互交換。這就是為什麼需要同時考慮這兩個比率，因為通常可以通過犧牲一個比率來提高另一個比率。為了解決這個問題，可以考慮一個更嚴格的標準，即當這兩個比率都大於1時，算法ℓ才被認為在硬件S上高效。

C. 阿姆達爾法則

在實踐中，算法由多個步驟組成，算法中的一部分計算可以在基於物理的ASIC上高效運行。例如，在卡爾曼濾波算法中，有矩陣求逆和矩陣-向量乘法（MVM），可能希望使用ASIC來處理矩陣求逆，而GPU用於處理矩陣-向量乘法。在這種情況下，阿姆達爾法則對使用ASIC所能獲得的性能提升設定了限制。設x為算法運行時間T中可以在ASIC上加速的計算所佔的比例。那麼，(1 − x)T是通過使用ASIC可以達到的最小運行時間，因此最大加速比僅為1/(1 − x)。對於能效的最大提升也可以進行類似的推理。

D. 算法協同設計

由於阿姆達爾法則，需要仔細思考如何為給定的硬件範式設計算法。舉個例子，關於今天AI應用中的SOTA算法，採取以下視角非常有趣。這些算法隱式地被協同設計用於特定的硬件平台，即GPU。例如，變換器（Transformers）理想地與GPU匹配，因為它們執行大量可並行化的矩陣運算，而GPU專門為並行矩陣運算而設計。從這個意義上講，GPU得益於一個龐大的研究者社區，他們為GPU平台共同設計了算法。

同樣，基於物理的ASIC也將受益於學術界在算法協同設計方面的研究。對於給定的算法框架，有超參數允許將複雜度從一個子程序推送到另一個子程序（例如，從採樣到優化，或從神經網絡的複雜性到動態系統的時間演化）。關鍵在於通過某種方式推動複雜度的轉移，從而增加阿姆達爾法則中出現的比例x。因此，必須將算法ℓ(h)視為僅在其超參數h的範圍內定義。此外，僅僅因為某些算法ℓ(h)在硬件S上未表現出性能優勢，並不排除通過調整複雜度來獲得修改後的算法ℓ(h′)，從而獲得性能優勢的可能性。因此，值得將方程式（1）和（2）中的性能指標替換為R̂T(ℓ) = maxh RT(ℓ(h))和R̂E(ℓ) = maxh RE(ℓ(h))，它們表示對所有協同設計算法ℓ與硬件S的努力進行最大化。

E. 物理機器學習

一種算法與硬件協同設計的方法是直接在硬件層面上進行機器學習——我們稱之為“物理機器學習”（PML）。PML通常涉及一個監督學習過程，其中通過直接優化硬件的可調物理參數（例如，可調導電性）來學習給定硬件所執行的計算，從而使得數據通過物理硬件的端到端轉換最佳匹配訓練數據集。在數學上，硬件的輸入數據x⃗通過某些可編程參數的子集進行編碼（例如，應用於硬件某部分的電壓，如輸入電流源），經過一段時間後，硬件物理自由度的（通常是不同的）子集被測量（例如，離開一組定義輸出線的電流），以產生輸出向量y⃗。物理機器學習的過程涉及使用優化算法來設置硬件的可控參數θ⃗，影響從x⃗到y⃗的有效計算，即y⃗ = fp(x⃗, θ⃗)，其中fp表示硬件時間演化所導致的輸入和輸出之間的轉換。

例如，可調參數可以是施加在輸入和輸出電流之間晶體管上的電壓，這些電壓改變電流在硬件中的流動方式。在許多形式的PML中，可調參數可能以數字預處理或後處理的形式進行編碼。例如，在物理水庫計算中——PML的開創性概念——物理轉化是（在最簡單的非遞歸情況下），y⃗ = W (θ⃗)fp(x⃗)。其中，W (θ⃗)是一個線性矩陣，通過線性迴歸學習得到。通過適當優化W的權重，所需的非線性函數可以通過“特徵”（即輸入x⃗的函數）的線性組合來近似，這些特徵是由物理硬件自然計算出來的（在物理水庫計算中被描述為“水庫”）。其他形式的PML學習物理硬件的參數，而不是（或除了）這種數字後處理，例如物理神經網絡、變分量子算法和“材料中”計算。

一方面，PML為硬件和軟件的聯合優化提供了一種潛在的優雅解決方案，因為算法實際上是直接從硬件本身提供的計算空間中學習的。然而，迄今為止，PML學習到的算法通常相當簡單，要麼是因為優化參數的過程非常困難，要麼是因為物理硬件本身的表達能力有限。PML中的優化之所以困難，部分原因是，與現代人工神經網絡不同，後者經過系統工程設計，能夠在應用隨機梯度下降法學習其參數時表現良好（例如，通過像殘差連接這樣的架構創新），物理硬件學習的工程工作較少，因此許多硬件假設（即fp的具體形式）呈現出更加具有挑戰性的優化景觀，表現出例如貧瘠的平坦區域，使得梯度下降法變得無效。此外，直接優化物理硬件會遇到困難，因為硬件通常與任何理想化的仿真不同——這種“仿真到現實”的差距意味着，僅通過仿真硬件來執行優化往往會失敗。

由於這些挑戰，PML子領域的一個重要開放問題是開發有效的學習算法，這些算法可以用在一個單獨的處理器中來高效配置θ⃗，或者——理想情況下——直接使用物理硬件來實現這一目的，即物理學習。

F. 物理學習

PML最強大的形式是同時在物理硬件中進行推理（即物理計算y⃗ = fp(x⃗, θ⃗)）和學習（即確定參數θ⃗的最佳選擇）。與僅執行推理的硬件相比，顯然設計可擴展硬件（以及可擴展學習算法）使得這兩個功能都能實現要更加困難。但克服這個困難無疑是值得的：解決物理驅動學習的挑戰可以實現令人矚目的可擴展基於物理的ASIC，這些ASIC可以直接學習執行所需的計算，甚至無需數字計算機的監督。這將允許緊湊、高效的神經網絡計算，具有比現代數字系統更多的可訓練參數。

對於電子硬件中的物理驅動學習，通常需要有局部規則來更新邊緣，就像大腦中的神經元根據局部條件自我更新，而不需要知道其他所有神經元的狀態一樣。這樣規則的一個重要類別已經為電子、流體或機械網絡開發出來，這些網絡根據優化原則進行平衡。在實驗室中的電子網絡上，每個邊緣上都已建立電路，實現局部學習規則以調整其電導。在訓練完成後，後續的計算（推理）僅通過提供輸入電壓來物理地完成，讓系統平衡，並讀取輸出電壓。設計問題然後涉及硬件和可調邊緣的選擇、學習電路、網絡架構，以及——重要的是——如何在芯片上大規模實現。物理學習還可以在各種其他系統中完成。

四、應用

圖5展示了基於物理的ASIC將影響的一些應用。這些設備天生適合受物理世界啓發或基於物理世界的應用。

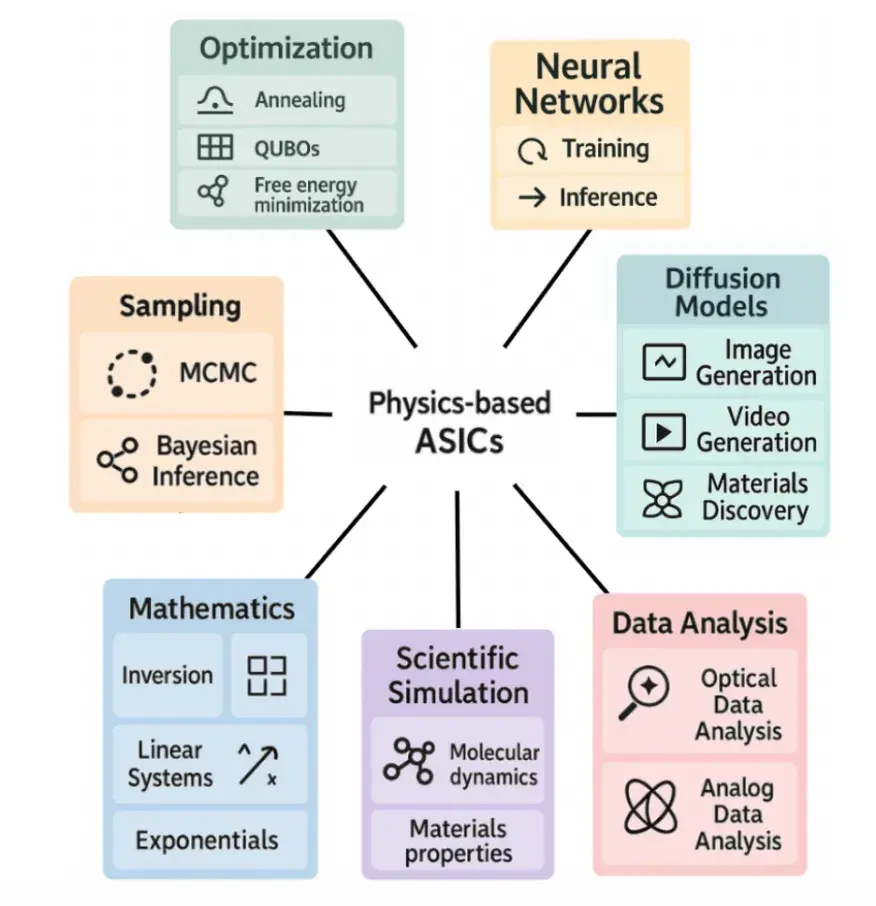圖 5. 基於物理的ASIC應用。 部分應用受物理啓發（如採樣和優化）。其他應用則基於物理原理（如科學模擬和模擬數據分析）。在數學領域的抽象應用也同樣相關。

A. 物理啓發的應用

許多算法受到物理啓發。這很可能是因為開發這些算法的人對物理有很強的直覺，並且歷史上物理學曾是早期的應用重點。儘管現代應用如AI和金融更加抽象，但它們在實踐中往往仍然使用物理啓發的算法。

1.人工神經網絡

2024年諾貝爾物理學獎授予了Hopfield和Hinton，以表彰他們為使人工神經網絡（ANNs）機器學習奠定基礎的工作。儘管關於人工神經網絡是否受到物理啓發或生物學啓發存在爭議，但早期的ANN，如Hopfield網絡和玻爾茲曼機，確實源自自旋系統的統計物理學。

儘管用於主流機器學習的人工神經網絡與大腦中的生物神經網絡差異巨大，但它們仍然非常適合在嘈雜的模擬硬件上進行計算。首先，現代的人工神經網絡在很大程度上依賴於一組有限的操作，這些操作會重複多次，如矩陣-矩陣和矩陣-向量乘法。這意味着，基於物理的ASIC可以加速這一類別中的有限計算，從而在神經網絡推理或訓練中提供顯著優勢。其次，雖然現代ANN通常在高精度數字計算機中實現，但它們已被證明對噪聲具有極強的抗性——ANNs通常可以被訓練以非常低的（甚至是二進制的）精度權重和激活值進行操作，並且幾乎沒有性能損失，同時訓練中常常使用噪聲（例如，採用dropout形式）來提高泛化能力，並使學習到的神經網絡對抗攻擊更加魯棒。最後，隨着更多計算資源的投入，ANNs表現出顯著的改進，例如通過增加可學習的參數數量（以及每次推理的計算量）、延長訓練時間或通過其他方法提高計算利用率。這些特性的結合使得ANNs特別適合通過專用的嘈雜模擬硬件加速，而它們快速擴展的應用表明，進行這種加速具有強大的商業驅動力。

2. 擴散模型

最明顯的物理啓發算法之一是擴散模型。關於這一主題的原始工作指出了與非平衡熱力學的深刻聯繫。由於隨機過程的時間反轉在隨機熱力學中經常被考慮，人們意識到相同的形式主義可以用來逆轉向數據添加噪聲的過程，從而形成生成模型。在過去幾年中，擴散模型已經成為一種生成圖像、視頻、分子結構和材料的最先進方法。硅中自然發生的隨機性使得基於物理的ASIC非常適合運行擴散模型。此外，擴散模型允許我們放寬確定性操作的限制，以便通過基於物理的ASIC實現更高效的性能。

3. 採樣

更廣泛地説，從期望概率分佈中進行採樣的問題可以通過使用物理啓發的算法來解決。像氣體或磁自旋這樣的物理系統自然地向平衡演化，其中微觀狀態遵循玻爾茲曼分佈，且一個狀態的可能性會被其能量指數級地抑制。現代的採樣方法模仿這一行為，從非物理領域（如機器學習或貝葉斯推斷）中的複雜分佈中生成樣本。像馬爾可夫鏈蒙特卡洛（MCMC）及其變種的算法模擬了物理系統中粒子的隨機遊走，並能夠在高維空間中高效地採樣。基於物理的ASIC有望使離散和連續變量的採樣更加高效，實際上是通過將採樣算法還原到其根源來實現。也就是説，這些ASIC使用實際的物理系統，其動力學（例如，熱力學放鬆）實現了Langevin蒙特卡洛、貝葉斯推斷或其他採樣協議。使用Ising機的概率計算和使用隨機電路的熱力學計算都是有前景的採樣應用方法。

4. 優化

優化也深受物理學啓發，因為物理系統自然地執行優化。熱力學系統朝向最小化自由能的配置演化，推動了相變，如晶體形成和蛋白質摺疊。自由能最小化的原則與搜索成本或損失函數全局最小值的優化算法相似，類似於物理系統穩定到其最穩定狀態的過程。例如，模擬退火明確模擬了金屬的冷卻過程，這一過程消除了原子級缺陷。一些基於物理的ASIC可以執行這種退火算法，其中一個抽象的損失函數被編碼為物理能量函數。類似地，Langevin動力學可以視為Wasserstein梯度流。基於物理的ASIC在Langevin動力學下演化，實際上是在Wasserstein空間（即概率密度函數的度量空間）中執行梯度下降，因此可以用於在概率分佈上進行優化。組合優化，涉及從離散可能性的集合中找到最佳解決方案，可以通過與Ising模型的關聯視為物理啓發。即，二次無約束二進制優化（QUBO）問題可以映射到Ising模型的能量函數。Ising機器利用這一深刻的聯繫高效地解決QUBO問題，並且可以擴展到混合變量優化。最後，基爾霍夫的電子電路定律可以解釋為一個優化問題，其中系統自然最小化能量耗散（受限於約束）。這一點已經被用來通過電阻網絡解決優化問題，電阻網絡作為一個基於物理的ASIC，既可以自我訓練，又可以執行所需的計算。

B. 基於物理的應用

1. 科學模擬

基於物理的ASIC最直觀的應用之一是模擬物理世界。設計新材料並預測其性能是一項令人興奮的任務，但對當前的計算硬件來説頗具挑戰。基於物理的ASIC可通過物理啓發的生成式AI（如擴散模型）和通過動態模擬強化材料特性表徵，加速材料發現。分子動力學（MD）模擬方法已廣泛應用於工業，例如在氨合成催化劑設計和環境保護中。費曼曾指出，我們應使用物理系統來模擬物理，而MD正是一個例子，基於物理的ASIC可加速分子和材料的動力學模擬。這包括加速Langevin動力學、傘形採樣以及躍遷路徑採樣等原語。我們還強調常被忽視的介觀模擬領域，在此量子效應消失，經典隨機熱力學成為合適框架。基於物理的ASIC將在介觀模擬中發揮關鍵作用（如納米結構材料的自組裝和非牛頓流體的流變學），很可能作為複雜工程過程多尺度建模的一個組成部分。在更深層次上，介觀層面還存在未解的科學問題，如生命的起源。基於物理的ASIC可用於驗證例如England的耗散驅動適應理論和基於物理的自我複製出現等機制，以解釋地球上生命的起源。

2. 模擬數據分析

基於物理的神經網絡在處理本質上為模擬形式的數據方面展現了希望。例如，光學神經網絡可自然地分析光學數據，對音頻數據或模擬電信號同樣適用。基於物理的神經網絡通過直接在模擬域執行分析，避免了將模擬信號轉換到數字域的開銷。隨着AI變得更加多模態並更多地與物理世界（如機器人技術）結合，這些應用將變得尤為重要。

五、路線圖與挑戰

我們預計基於物理的ASIC的採用將分為三個階段。第一階段，各研究團隊將利用概念驗證硬件展示其基於物理的ASIC架構在性能上優於在CPU和GPU上運行的最先進方法。接下來，需要解決關鍵的可擴展性問題，使基於物理的ASIC能夠處理與現有硬件解決方案相當規模和複雜度的問題。最後，這些擴展後的基於物理的ASIC需要集成到系統中，並設計軟件抽象，以便輕鬆運行關鍵計算工作負載。

階段一：展示領域特定優勢

基於物理的ASIC採用的最重要驅動力是其在運行關鍵計算工作負載時的性能和能效。因此，任何基於物理的ASIC項目的首要目標之一，應當是展示在某個關鍵工作負載上優於傳統CPU或GPU方法的可行路徑。

關鍵應用的加速

對於某些問題，規模相對較小的基於物理的ASIC原型能夠表現出優於CPU或GPU求解器的性能。例如，對於具有1440個Ising自旋的問題，基於鎖存器的Ising機在最小化Ising哈密頓量方面，比CPU求解器快1000倍以上。然而，對於更大規模的問題，由於將數據加載到物理ASIC以及從中讀取的成本，這些原型往往無法達到同樣的加速效果。這凸顯了內存帶寬和可擴展性是原型系統的關鍵瓶頸。

另一種證明潛在加速的方法是展示關鍵的規模優勢。例如，基於耦合振盪器的模擬Ising機預計在約150個自旋或更大規模時就能超過GPU求解器的性能。同樣，與最先進的數字方法相比，熱力學計算在線性代數和貝葉斯推斷任務上具有更優的漸近複雜度，這些複雜度優勢亦可延伸到神經網絡訓練等更高層次的應用，而後者在GPU上計算成本極高。

儘管如此，過去摩爾定律的進展主要來自於縮小規模前置因子，而並非改變漸近複雜度。因此，旨在優化前置因子的傳統工程創新仍然至關重要。

能效

基於物理的ASIC由於可將某些應用更自然地映射到物理硬件，因此在能效方面也有望遠超GPU求解器。研究表明，光學神經網絡在執行每次標量乘法時探測的光子數不到一個，這比基於數字電路的傳統方法具有根本性的能量優勢。同樣，一種帶有全連通耦合振盪器的模擬Ising機在解決組合優化問題時，其能耗比在CPU上運行的最先進算法低1–2個數量級。此外，在由自調整電阻構成的模擬電子網絡中進行物理計算，相較於數字計算，能效節省潛力可達百萬倍。

階段二：構建可擴展物理基底

文獻中展示的大多數基於物理的ASIC規模相對較小，尤其與傳統數字硬件相比。這些工作對於證明基於物理的ASIC概念的可行性非常寶貴，但仍需額外工作，將這些設計擴展到能夠解決具有工業意義的現實問題的程度。

基於tile的ASIC設計

例如，提出了“可現場編程的Ising陣列”，利用基於tile的層級結構來實現更高的效率和可重構性。每個tile包含密集的全連通模擬耦合，而tile間的連接則完全由數字通道組成且較稀疏。這限制了模擬耦合電路的規模，從而防止了寄生效應和噪聲對其性能的顯著退化。基於tile的架構以及其他層級架構在物理實現方面也具有實際優勢。tile設計可以獨立於其他tile進行設計、綜合和佈線，然後置於片上網絡（NoC）中與其他tile通信。當每個tile包含模擬或混合信號組件時，這一點尤為重要；如果沒有層級架構，要在GPU規模和複雜度上設計並仿真混合信號芯片將極其困難。

可重構交互項

許多基於物理的ASIC也難以支持密集型問題。它們通常只能支持固定的圖拓撲，需要軟件將任意問題映射到該固定拓撲。這一過程稱為次要嵌入，其計算開銷高昂，並且可能在大規模或複雜問題上失敗。顯然，需要更好的硬件支持來應對不同稀疏模式的圖結構。

為此，提出了一種p比特計算架構，使用可重構的主圖來支持不同稀疏模式的圖。這種方法保留了稀疏連接的可擴展優勢：每個p比特的鄰居數量保持不變，因此硬件利用率隨規模線性擴展，且隨着p比特數量增加，最大工作頻率保持大致恆定。

通過利用模塊化、可tile化的計算單元和可重構耦合，基於物理的ASIC有望擴大到與GPU相當的規模，同時支持多種不同稀疏模式的問題。

階段三：集成到混合系統

一旦展示出大規模的基於物理的ASIC，就需要從硬件和軟件兩方面將其集成到實用的大規模系統中。

異構硬件平台

由於基於物理的ASIC專門用於解決某些類型的計算問題，我們預計它們將部署在所謂的異構系統中，與傳統GPU和CPU協同工作。例如，曾提出一種超級計算系統，結合了多台網絡化的概率處理器、傳統GPU和量子處理器。這樣的系統能夠高效加速能量基模型（EBM），使用GPU處理大型矩陣‑向量運算（如嵌入計算和梯度計算），同時使用概率處理器模擬神經元的隨機操作。

標準軟件抽象

為了使基於物理的ASIC獲得廣泛採納，它們需要對不熟悉底層物理過程的軟件工程師友好。實際上，這意味着基於物理的ASIC應利用用户已熟悉的標準軟件抽象，如PyTorch和JAX。例如，已經為電學和光子Ising機開發了基於Python的編程模型。為了讓用户在基於物理的ASIC上運行更復雜的工作負載，可能需要一個編譯層。我們的願景是，用户只需在PyTorch或JAX中編寫一個程序，即可自動編譯並在由CPU、GPU和基於物理的ASIC組成的混合系統上運行，使每種芯片都用於其最擅長的工作負載部分。

六、結論

A. 領域願景

隨着傳統擴展進入平台期，基於物理的ASIC不僅提供了一種可行的替代方案，更是計算方式的必要演進。這個新興領域利用自然的物理過程，而不是對抗它們。標準計算為了滿足抽象出硅物理特性的假設，消耗了大量能源。通過放寬這些假設，我們的領域旨在解決當今計算硬件中的不可持續能耗。此外，我們致力於加速那些制約AI工作負載的關鍵應用：採樣、生成式AI、優化、神經網絡訓練與推理，甚至其他物理系統的模擬。

未來的道路不會由單一架構或通用解決方案定義。可以想象，高性能計算（HPC）平台將由多個基於物理的ASIC組成，每個ASIC專注於不同角色。例如，多尺度物理建模的HPC平台可以集成在原子級、微觀、介觀和宏觀四個層次上運行的ASIC，每個層次的硬件都針對其物理範疇進行優化。同樣，面向模型的強化學習HPC平台也可由異構計算堆棧構成，針對特定應用進行性能優化，不同ASIC分別負責採樣、優化和物理仿真等子程序。

能量和時間在物理學中具有基礎性作用，在計算中亦然。這並非巧合，因為物理為評估計算性能提供了統一框架。例如，能量‑時間權衡（更廣義的能量‑時間‑精度權衡）在基於物理的ASIC中自然而然地出現，同樣也適用於理解標準數字計算的複雜性。這暗示了對計算複雜性進行統一處理的可能性，這將是平等比較不同計算範式的關鍵。

基於物理的ASIC為超越傳統擴展極限的計算提供了新途徑。在未來兩年內，我們預計會看到越來越多的實驗證明基於物理的ASIC相較於標準硬件具備性能優勢。初期的驗證或將展示在相同性能水平下的巨大能效提升，而後續演示可能解鎖標準硬件無法實現的新功能。這些新功能或包括可擴展的無近似貝葉斯推斷以支持可靠的AI預測、大規模高精度分子動力學模擬，或在邊緣設備中實現對模擬物理數據的快速分析。

B. 行動呼籲

實現這一願景將受益於一個活躍、不斷壯大的熱情開發者社區。我們重點指出了以下幾個需要採取行動的關鍵領域：

識別一組GPU不擅長的應用。 GPU擅長並行計算，但不一定擅長順序計算。例如，模擬物理動力學應用在時間上是順序的，對GPU而言具有挑戰性。雖然許多物理模擬可以在子系統（如單個粒子）之間並行化，但僅靠並行處理所能獲得的性能優勢是有限的；總體運行時間始終受限於最長順序步驟鏈長度與單步延遲的乘積。因此，在高度並行的場景中，性能最終將受制於仿真步驟的時延，而非總計算吞吐量。

為基於物理的ASIC協同設計算法。 變換器已與GPU共同設計。我們的領域同樣需要算法與應用社區的廣泛參與，開發新算法，並在已有算法中重新分配複雜度，以提升基於物理的ASIC的性能優勢。

構建基於物理的ASIC全棧。 這一新硬件需要編譯器和用户界面，以獲得社區的廣泛採用。開源軟件可能是推廣應用的關鍵要素。此外，為基於物理的ASIC開發模擬器將有助於普及這一領域。

以無需物理或電氣工程背景也能理解的方式闡釋我們的目標與方法，降低與計算機科學家之間開展有意義交流的門檻。

C. 領域的緊迫性

最後，我們認為，社會面臨的與計算相關的危機——從AI能源危機到計算成本危機，再到關鍵擴展定律的終結——賦予了我們這一領域緊迫性。多重危機可通過單一技術來應對，這為我們提供了獨特的機遇。此外，這一技術也受到AI異常快速崛起的推動。顯然，AI已成為催生基於物理的ASIC這一新領域的經濟驅動力，因此這兩個領域密切相關。隨着AI不斷向物理世界靠近，基於物理的ASIC未來有望為AI提供物理化身。

「致謝本文作者」