傳奇數學家生前最牽掛的謎題終獲解_風聞
返朴-返朴官方账号-科普中国子品牌,倡导“溯源守拙,问学求新”。38分钟前
 2024年底,兩位數學家肯定地回答了傳奇數學家讓·布爾甘關於高維凸形狀的“簡單”問題。值得一提的是,他們的工作建立在中國數學家關慶揚近期的突破之上。另一方面,對於凸幾何體截面的研究歷史,或許要追述到400餘年前歐洲一位傳奇貴族的賭約。
2024年底,兩位數學家肯定地回答了傳奇數學家讓·布爾甘關於高維凸形狀的“簡單”問題。值得一提的是,他們的工作建立在中國數學家關慶揚近期的突破之上。另一方面,對於凸幾何體截面的研究歷史,或許要追述到400餘年前歐洲一位傳奇貴族的賭約。
撰文 | 嘉偉
魯珀特問題:立方體穿洞
Prince這個英語單詞,現在有不分語境統統翻譯成王子或親王的趨勢,其實很多情況應譯成(地方的)邦君一類。不過馬上要介紹到的Prince Rupert,則是貨真價實的普法爾茨的魯珀特親王(Prince Rupert of the Rhine, Duke of Cumberland)。
這位400年前的歐洲貴族是一位發明家、藝術家,也是一位戰功彪炳的戰士,幾乎能流利使用歐洲所有主要國家的語言,在數學方面也有兩把刷子。
 普法爾茨的魯珀特親王,軍人、政治家、私掠船船長和科學家丨圖源:Prince Rupert of the Rhine - Wikipedia
普法爾茨的魯珀特親王,軍人、政治家、私掠船船長和科學家丨圖源:Prince Rupert of the Rhine - Wikipedia
魯珀特親王在17世紀提出了一個至今仍被津津樂道的幾何問題。這個問題的由來頗具傳奇色彩:他曾與人打賭,聲稱可以在一個立方體上開一個洞,然後讓另一個同等大小的立方體穿過這個洞。
當時的人們普遍認為這不可能實現,直覺告訴我們,一個立方體怎麼可能穿過一個同樣大小的立方體上開的洞呢?然而,魯珀特親王最終贏得了這筆賭金。(至少故事是這麼講的,但歷史上是否確有其事還存有疑問。實際上,這個開洞模型所需的加工精度,以當時的技術似乎無法做到。)
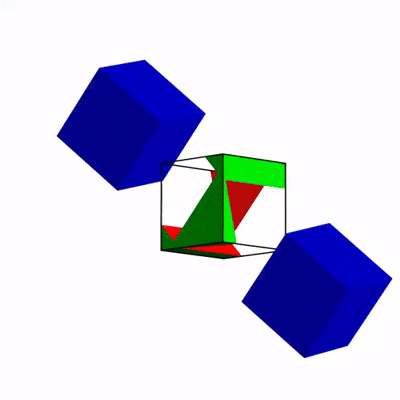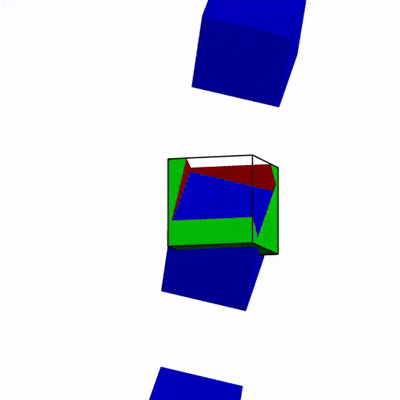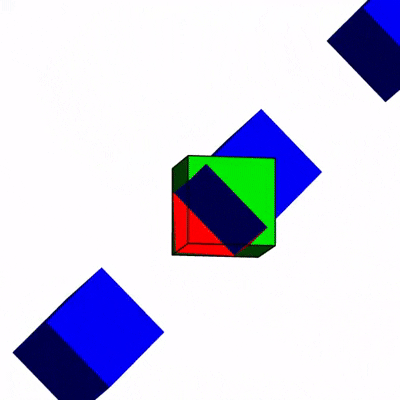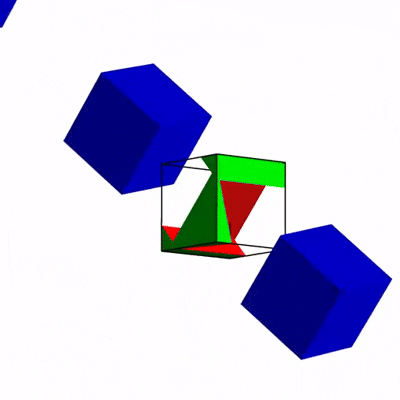 立方體穿過等大小立方體上的洞。| 圖源:科幻作家格雷格·伊根
立方體穿過等大小立方體上的洞。| 圖源:科幻作家格雷格·伊根
問題的核心在於對“洞”的理解。由於立方體是一種簡單凸多面體(“凸”是指構成幾何體的點集合中任意兩點連線,線段上的點也完全包含在該集合中),我們可以從投影入手:設想在正午陽光的垂直照射下,立方體的邊緣輪廓會在地面投下影子,能否調整立方體方向,使影子可以容納足夠大的內接正方形呢?正方形截面與“內方塊”穿過的直線運動方向正交,截面本身就是打洞的輪廓。理解這一點是解決問題的關鍵。
不妨假設,當投影面積最大時,更容易找到正方形截面。此時投影沿立方體的體對角線方向,影子是一個正六邊形。可以從這一方向穿越立方體的最大正方形(也就是可穿過的立方體的側面),就巧妙地“隱藏”在這個正六邊形內部。
我們還可以進一步提問:等大的立方體可以穿過,更大的立方體行不行?對於單位立方體,可穿過的立方體最大能有多大?
歷經一個多世紀,上述問題才得到解決。第一個在書面上提到這個謎題的是約翰·沃利斯(John Wallis),他在1685年發行的《代數論著》(De Algebra Tractatus)中收錄了
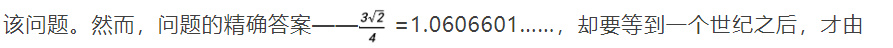 荷蘭數學家彼得·紐蘭德(Pieter Nieuwland,1764—1794)給出。紐蘭德證明,只要從單位立方體的四條稜上各取距頂點3/4的位置作四點,這四點恰好形成一正方形,沿此正方形的法向挖通孔道,就是問題的最優解。這個答案是在紐蘭德過世後的1816年,由他的老師揚·亨德里克·範·史温登(Jan Hendrik van Swinden)在整理他留下的論文集時意外發現的。
荷蘭數學家彼得·紐蘭德(Pieter Nieuwland,1764—1794)給出。紐蘭德證明,只要從單位立方體的四條稜上各取距頂點3/4的位置作四點,這四點恰好形成一正方形,沿此正方形的法向挖通孔道,就是問題的最優解。這個答案是在紐蘭德過世後的1816年,由他的老師揚·亨德里克·範·史温登(Jan Hendrik van Swinden)在整理他留下的論文集時意外發現的。
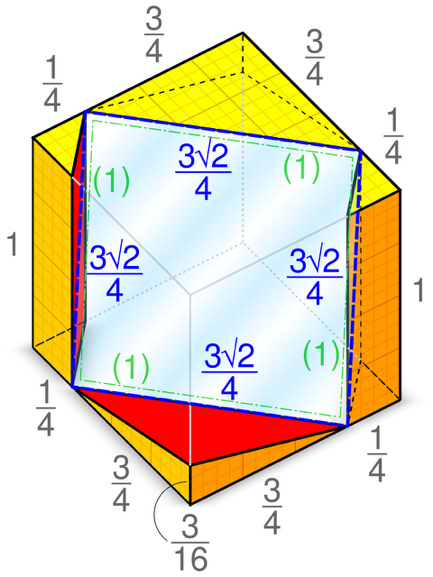 紐蘭德的最優解 | Wikipedia
紐蘭德的最優解 | Wikipedia
數學家不會滿足於僅僅解決一個具體的問題,他們推廣出更普遍的幾何概念——“魯珀特性質”(Rupert property)。“魯珀特”變成了一個形容詞:一個幾何體如果能被一個同等或更大尺寸的自身副本穿過,那麼它就是魯珀特的。這個概念將魯珀特親王最初的立方體問題推廣到了更廣泛的多面體乃至高維空間。
目前我們知道,柏拉圖多面體(凸正多面體)都具備此性質,所有n維超正方體也是如此。
到2019年,數學家證明截角四面體是魯珀特的。
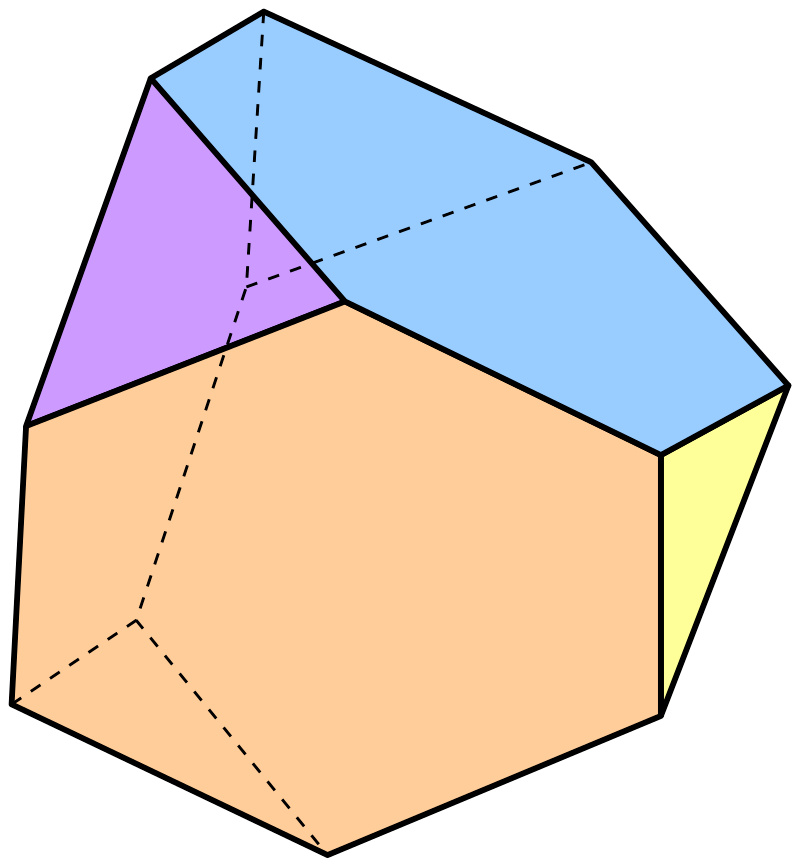 截角四面體是將一個正四面體的四個頂點切去得到的形態。| 圖源:Truncated tetrahedron - Wikipedia
截角四面體是將一個正四面體的四個頂點切去得到的形態。| 圖源:Truncated tetrahedron - Wikipedia
截角四面體屬於阿基米德多面體(Archimedean solids)。後者是幾何學中一類非常優雅的凸多面體,它們的面都是正多邊形,且每個頂點的鄰接方式完全相同,但與柏拉圖多面體不同的是,它們的面可以由多種不同類型的正多邊形組成。共有13種阿基米德多面體,而已知其中9種都是魯珀特的。
另外,根據數學家理查德·蓋依(Richard Guy)與理查德·諾瓦科斯基(Richard Nowakowski)的研究結果,能夠穿過4維超正方體的最大超正方體,其邊長為1.007434 775…,即1.014924…的平方根,1.014924…也是一元四次方程4x^4-28x^3-7x^2+16x+16=0的最小實根。
有人推測所有凸多面體都是魯珀特的,沒有例外。但我想證明一定非常難。
數學巨匠讓·布爾甘的猜想
400年前的魯珀特問題,本質上就是探究多面體可能的最大斜截面。20世紀的數學家則從完全不同的角度來思考體積固定,但形狀可變的高維凸幾何體的最大截面的一致下界。
在1980年代研究最大函數(maximal function,現代分析學中的工具)的背景下,數學家讓·布爾甘(Jean Bourgain)提出了一個關於高維形狀的“簡單”問題,這便是著名的“布爾甘切片問題”:是否存在一個常數c>0,使得對於任何維度n和任何體積為1的凸體K,都存在一個超平面H,使得K ∩ H的(n-1)維體積至少為c?
簡單來説,這個問題問的是:如果一個凸體的體積是單位體積,那麼它是否一定存在一個“足夠大”的低一維切片?
乍一看,和略反直覺的魯珀特問題不同,布爾甘猜想似乎是顯然的。畢竟,如果幾何體的形狀在各個方向都非常細,它怎麼可能佔據足夠的空間來形成一個體積單位呢?“得了吧——這能有多難?”高維幾何學家羅南·埃爾丹(Ronen Eldan)回憶起第一次聽説這個問題時的想法:“可你越思考,就越能體會到它其實有多麼精妙。”
讓·布爾甘被譽為傳奇數學家,這源於他在多個數學核心領域做出的深遠而變革性的貢獻,以及他獨特的研究風格和影響力。作為數學界的最高榮譽——菲爾茲獎(Fields Medal)的獲得者,他以非凡的問題解決能力而聞名。數學家陶哲軒曾評價説:“我的早期工作可以概括為——讀讓的論文,學會他的技巧,嘗試做些改進。”
 Jean Bourgain於1980年代拍攝的照片丨圖源:IHES
Jean Bourgain於1980年代拍攝的照片丨圖源:IHES
然而,即使是這樣一位卓越的數學家,也未能在有生之年完全解決自己提出的關於高維凸體切片的問題。
特拉維夫大學的維塔利·米爾曼(Vitali Davidovich Milman)是以色列數學界的重量級人物,在凸幾何、泛函分析和高維空間理論方面作出了奠基性貢獻。他曾寫道:“讓告訴我,他在這個問題上投入的時間和付出的努力,比他研究過的任何其他問題都多。”
布爾甘於2018年去世。就在去世前幾個月,他還詢問米爾曼,這個問題是否有進展。“他想在離開之前聽到答案。” 米爾曼回憶道。
直面古怪的高維世界
高維世界裏物體的行為方式往往違揹我們人類在低維宇宙裏養成的直覺。如高維質量集中現象:高維球的體積集中在它外圍很薄的一層球殼上,高維立方體的體積集中在它的一堆角上(微積分求極限可得),高維的高斯正態分佈從球面座標看,它的質量集中在一層半徑較大的薄薄的球殼上(用變分法可得)。
後一結論在概率論和實際應用上非常有價值,從此我們在高維情形下只需要考慮距離原點1-ε到1+ε的一層球殼就可以了,因為其餘部分的概率近似為0。
藉助這些結論可以立刻推知一些原本難以計算的概率極限。
比如説,n維立方體裏隨機兩點,隨着n增大取極限,隨機兩點的距離小於1的概率極限為0。
為什麼呢?因為如前所述,點都集中在超正方體的角上,也就是n越大,立方體內的點越接近超正方體的頂點。這就導致所謂任意兩點的距離,非常接近兩個頂點之間的距離。而超正方體兩個頂點間的距離最小就是1。
 四維超正方體示意圖丨Tesseract - Wikipedia
四維超正方體示意圖丨Tesseract - Wikipedia
再提供一個與切片猜想相關的問題——Busemann–Petty問題。這也是凸幾何中的經典問題,提出於1956年。它探討的是高維空間中截面體積與整體體積之間的關係,看似直觀,卻在高維中展現出極大的複雜性:設有兩個中心對稱的凸體(即關於原點對稱),如果一個凸體的所有經過中心的截面都比另一個大,那它的整體體積是否也更大?
在二維到四維空間中,這個直覺是正確的。然而令人驚訝的是,這個結論並不適用於五維及以上維度!這意味着,在五維及以上的空間中,存在這樣一種反直覺的可能:一個凸體的所有中心切面都比另一個小,但它的總體積卻更大。
正是高維的複雜性使得布爾甘切片問題遠非表面上那麼簡單,這也是高維幾何的美妙之處。可以説,布爾甘的切片猜想是“馴服”古怪高維世界的一次嘗試:至少在某些方面,高維幾何形狀也應順應我們的直覺。
此外如同前面提到的高維正態分佈,高維幾何的核心應用之一就是藉助幾何視角賦予多元概率直觀的形象,簡化期望、方差等數據特徵的計算;反之,概率論提供了一種理解高維幾何的新方式——利用概率工具來估算幾何對象的度量屬性(面積、體積等),是現代幾何學的重要研究方法。布爾甘則是這種研究傳統的開創者之一。他的“切片猜想”,這個樸素且看似明顯的問題為高維幾何學確立了新的方向。
米爾曼評價説,自布爾甘提出這個問題以來,它已成為學者理解高維凸體諸多問題的“敲門磚”。高維凸體不僅是純數學家關心的對象,也吸引了統計學家、機器學習研究人員以及其他需要處理高維數據集的計算機科學家的廣泛興趣。
里程碑式的突破
2024年12月,以色列魏茨曼科學研究所的博阿茲·克拉塔格(Bo’azKlartag)和法國普瓦捷大學的約瑟夫·勒埃克(Joseph Lehec)撰寫了一篇論文“Affirmative resolution of Bourgain’s slicing problem using Guan’s bound”,宣告這一長期懸而未決的問題,獲得了肯定的解答。
論文標題裏提到的“Guan’s bound”,是指中國科學院的數學家關慶揚得到的一個結論。關慶揚的工作建立在一種名為隨機局部化(stochastic localization)的技術之上。該方法最初由羅南·埃爾丹在其博士論文中提出,並在後續由其他學者進一步完善。
這種幾何方法也可以用物理學中的熱流解釋。該技術涉及在凸性假設下,運用隨機分析方法,對定義在n維歐氏空間中的概率測度的熱流演化過程給出精確估計。
埃爾丹憑藉此項工作拿到2023年新視野獎。同年獲獎者還有解析數論領域的領導者之一、菲爾茲獎得主詹姆斯·梅納德(James Maynard)。
現代學者幾乎不直接考慮高維凸體所有截面的面積/體積,轉而研究一個名為凸體迷向常數(Isotropic Constant)的量:這是衡量凸體“大小”的另一種方式(“迷向”意思是分不清方向)。簡單來説,原本是證明最大可能切片存在下界,此時則變成證明不同維度的凸體迷向常數有一個上界。同時雖然該定義具有更復雜的形式,但也因此具備了信息和概率意義。我們能夠直接對它應用信息論和概率論中的理論工具。
 克拉塔格和勒埃克作為高維凸體切片猜想的權威,對這一問題有深刻的理解。他們立刻意識到,關慶揚的結果就像是一把鑰匙,能打開解決切片猜想的最後一扇門。實際上,看到關的論文後,克拉塔格和勒埃克僅用幾天就解決了之前40年未能攻克的難題。克拉塔格指出:“很幸運,因為我們知道關慶揚的結果正是我們所需的要素之一。”
克拉塔格和勒埃克作為高維凸體切片猜想的權威,對這一問題有深刻的理解。他們立刻意識到,關慶揚的結果就像是一把鑰匙,能打開解決切片猜想的最後一扇門。實際上,看到關的論文後,克拉塔格和勒埃克僅用幾天就解決了之前40年未能攻克的難題。克拉塔格指出:“很幸運,因為我們知道關慶揚的結果正是我們所需的要素之一。”
他們結合米爾曼的M-橢球理論、隨機局部化技術以及關慶揚最新得到的參數上界,利用Eldan-Mikulincer的Shannon-Stam不等式穩定性估計,最終確立了凸體迷向常數有界(與維度n無關)的關鍵定理,一舉證得布爾甘的切片猜想。(M-橢球理論大致上是説,對於任何凸體K,都存在一個橢球E,使得二者在某種意義上相互“覆蓋”得很好。)
 Bo’azKlartag對這個猜想、它的歷史、證明的一些成分以及仍然懸而未決的相關猜想進行了精彩的演講。未來甚至有可能確定常數c的精確值。|圖源:Qingyang Guan, Joseph Lehec and Bo’az Klartag Solved The Slice Conjecture! | Combinatorics and more
Bo’azKlartag對這個猜想、它的歷史、證明的一些成分以及仍然懸而未決的相關猜想進行了精彩的演講。未來甚至有可能確定常數c的精確值。|圖源:Qingyang Guan, Joseph Lehec and Bo’az Klartag Solved The Slice Conjecture! | Combinatorics and more
克拉塔格半開玩笑地表示:“要是相信所謂的‘維度詛咒’,我們可能早就放棄了。好在,我和勒埃克屬於不同的學派。”
維度詛咒,從機器學習的角度來看,是指隨着數據集維度的增加,要想在不過度擬合的情況下對數據進行精確建模(即不記憶樣本的具體細節),所需的數據量會增長得非常快。因為即使數據集非常龐大,最終也只能覆蓋極其稀疏的整體可能性空間。舉例來説,用100個平均分佈的點採樣一個單位區間,相鄰點距離不超過0.01;而當維度增加到10後,如果以同樣的間距採樣一單位超正方體,則需要1020個採樣點。
如今,理論上的突破不僅為高維幾何學帶來了新的理論基礎,也為處理高維數據集的統計學、人工智能的機器學習和計算機科學等應用領域提供了更深刻的理解和新的工具。
比如説,當我們討論凸幾何體的截面時,是不是會讓人聯想起醫學影像和地質勘探中的斷層掃描?實際上,“幾何層析成像”正是一門通過分析幾何對象在各個平面上的投影(陰影)或橫截面數據,來重建其整體形狀的數學方法。
此外,為了解決切片問題,以及更強的KLS(Kannan–Lovász–Simonovits)猜想,數學家發展出一整套的概率方法。它們已經開始反哺統計學和信息科學,並在現實中發揮威力:這些研究告訴我們,在凸形空間中,即使用最樸素的隨機遊走,也能在顯著更少的步數內把行走位置分佈逼近均勻;這為所有基於隨機遊走的高維算法提供了堅實、可量化的性能下限,幫助計算機科學家在各種隨機採樣技術之間確定優先級——弄清楚什麼時候最基本的隨機遊走就已足夠,何時則應選擇更復雜、計算成本更高的算法以獲得更佳性能。
最後,我想每個人都會同意,布爾甘會對這一結果感到欣慰。
後記
雖然博阿茲·克拉塔格是凸幾何領域裏的世界級權威學者,長期研究高維對稱結構,此前從未正式涉足晶格/格點理論(Lattice Theory)領域。然而,晶格其實一直是他渴望去研究的對象。
就是在證明了布爾甘的切片猜想之後,他意識到:“我已經47歲了,我一生都想研究格,如果我現在還不去做,那就永遠不會去做!”
隨後克拉塔格開始了自己的“圓夢之旅”。在今年4月,他以局外人未受到既有研究侷限的視角,憑藉對凸幾何的理解與隨機過程的掌握,在離散幾何領域又迅速得到了一個里程碑式的成果。不過,那就是另一個故事了。
參考文獻
[1]Rupert property of Archimedean solids. The American Mathematical Monthly, 125(6), 497–504.
[2]The n-Cube is Rupert.The American Mathematical Monthly, 125(6), 505–512.
[3]The truncated tetrahedron is Rupert. The American Mathematical Monthly, 126(10), 929–932.
[4]Affirmative resolution of Bourgain’s slicing problem using Guan’s bound. arXiv preprint arXiv:2412.15044.
[5]A note on Bourgain’s slicing problem. arXiv preprint arXiv:2412.09075.
[6]Bourgain’s slicing problem and KLS isoperimetry up to polylog. arXiv preprint arXiv:2203.15551.
[7]Qingyang Guan, Joseph Lehec and Bo’az Klartag Solved The Slice Conjecture! | Combinatorics and more
[8]EricaKlarreich, Statistics Postdoc Tames Decades-Old Geometry Problem
注:本文封面圖片來自版權圖庫,轉載使用可能引發版權糾紛。
 特 別 提 示
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。
版權説明:歡迎個人轉發,任何形式的媒體或機構未經授權,不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。