瑞利:振動理論的開拓者與傳播者_風聞
返朴-返朴官方账号-科普中国子品牌,倡导“溯源守拙,问学求新”。1小时前
 英國物理學家瑞利是19世紀重要的物理學家,但很多人對他的成就並不瞭解,或許只知道他提出的瑞利散射(可以解釋為什麼天空是藍色的),以及瑞利-金斯公式(為了解普朗克黑體輻射定律作為鋪墊)。事實上,瑞利在經典物理學多領域有傑出貢獻,特別是對振動理論有開創性貢獻;合作發現氬(獲1904年諾貝爾獎),其研究推動了多個學科發展。
英國物理學家瑞利是19世紀重要的物理學家,但很多人對他的成就並不瞭解,或許只知道他提出的瑞利散射(可以解釋為什麼天空是藍色的),以及瑞利-金斯公式(為了解普朗克黑體輻射定律作為鋪墊)。事實上,瑞利在經典物理學多領域有傑出貢獻,特別是對振動理論有開創性貢獻;合作發現氬(獲1904年諾貝爾獎),其研究推動了多個學科發展。
撰文 | 陳立羣(上海市應用數學和力學研究所,上海大學 力學與工程科學學院力學系)
瑞利 (Lord Rayleigh, 1842—1919) 本名約翰•威廉•斯特拉特 (John William Strutt),承襲父爵為第三代瑞利男爵 (3rd Baron Rayleigh),是英國物理學家,諾貝爾物理學獎獲得者。瑞利在經典物理學的力學、電學、熱學和光學各個領域都有傑出貢獻。他的科學論著包括一部兩卷本專著《聲的理論》(The Theory of Sound)[1-2]和466篇論文,論文收入6卷本文集[3-8],其中前5卷由瑞利親自審定並加少量註記,最後1卷在瑞利身後出版。
瑞利的眾多科學成就,包括對振動理論的開拓性貢獻。在瑞利的時代,振動理論還沒有形成獨立的框架,部分內容屬於應用數學,部分內容屬於實驗物理,部分內容屬於聲學。正是由於瑞利等開拓者的理論貢獻,以及後續工程技術發展的強烈需求,振動理論作為力學分支學科應運而生。然而,瑞利對振動理論的貢獻在現有文獻中未見專門研究。本文側重分析瑞利對振動理論的創新貢獻,並説明《聲的理論》的特點。作為背景資料,還概括了瑞利的職業生涯和其他科學成就,這部分內容取材於瑞利兒子所撰寫的內容豐富生動的瑞利生活傳記[9],以及《聲的理論》美國版的導言作者對瑞利及其工作的概述[10]。還需要説明,本文提及瑞利論文,都引自論文集[3-8], 而不是論文發表的期刊。由於篇幅所限,與瑞利工作相關的他人工作都沒有給出具體出處。
職業生涯和科學成就
1842年11月12日,瑞利出生於英國埃塞克斯郡的富庶貴族家庭。其父是第二代瑞利男爵, 擁有超過28 km^2的特林莊園。瑞利自幼體弱多病,曾就學於著名的伊頓公學和哈羅公學,但都由於健康原因很快退學。後來他在小型私立寄宿學校完成中學教育。1861年,20歲的瑞利進入劍橋大學三一學院,導師是力學家勞斯 (Edward John Routh, 1831—1907),但他從數學家斯托克斯(George Gabriel Stokes, 1819—1903) 的數學課受益尤多。斯托克斯是盧卡斯數學教授 (牛頓曾經擔任的職位),但對實驗感興趣,並在課堂上進行演示。1865年,瑞利在劍橋的數學競賽上獲獎,同年獲得學士學位。到大學畢業時,瑞利不顧家族的質疑,決定從事科學研究。1866年,他當選三一學院住院成員,這是提供給獨身男士的帶薪職位。該職位有筆供出國訪學的經費,通常到歐洲大陸,但瑞利在1867年去了當時南北戰爭剛結束的美國,並於1868年返回後獲得碩士學位。
從1868年起,瑞利建設實驗室並開始科研工作。劍橋大學當時實驗基礎較為薄弱,1871年才設立實驗物理學卡文迪許教授講席,該職位由著名物理學家麥克斯韋 (James Clerk Maxwell, 1831—1879) 任職。麥克斯韋隨後出任卡文迪許實驗室主任。1871年瑞利因結婚而離職,新娘伊夫琳•鮑爾弗 (Evelyn Balfour, 1846— 1934) 是同學的妹妹。那位同學從政後曾任英國首相,是丘吉爾的政敵。瑞利夫婦有4個兒子,長子承襲男爵爵位並在倫敦帝國理工學院擔任物理學教授,是瑞利傳記[9]的作者。出於健康考慮,1872年秋瑞利夫妻去埃及旅行。1873年春他們返回英國,因父親去世瑞利繼承爵位和特林莊園,同時開始在莊園中建立個人的實驗室。1879年,瑞利接受劍橋大學任命,接替英年早逝的麥克斯韋,出任卡文迪許講席教授和實驗室主任。教授的職責是每年至少在校園18周並講40次課。在這期間,瑞利在實驗室的主要助手是他妻妹,當時很少的女性科技工作者。1884年,瑞利辭去劍橋大學教職,回到特林莊園繼續在個人實驗室中進行研究工作。1885年至1896年,他擔任倫敦皇家學會書記。1887年至1905年,他擔任大不列顛皇家研究所自然哲學教授,在任期內做過110次科普講座。1905年至1908年擔任倫敦皇家學會會長。1908年直到逝世他任劍橋大學校長,1909 年到逝世期間同時擔任政府航空顧問委員會主任。1919年6月30 日,瑞利在特林莊園因突發心臟病去世。
瑞利在經典物理學多個領域都作出傑出貢獻。除下節詳細分析的對振動理論的貢獻外,其他主要科學成就簡述如下。瑞利首次從理論上論述了直徑遠遠小於光波長的粒子對光的彈性散射即“瑞利散射”,由此可以説明天空為什麼是藍色的。他在研究地震時指出聲波在彈性固體中傳播時能量可能集中於表面附近的橫向表面波即“瑞利波”。瑞利對流體動力學作出了廣泛貢獻, 提出了與自然對流相關的無量綱數,即瑞利數,還提出了氣動升力的環流理論,相關貢獻還有瑞利流、瑞利-泰勒 (Sir Geoffrey Ingram Taylor, 1886—1975) 不穩定性和泰勒-庫埃特 (Maurice Couette, 1858—1943) 流穩定性的瑞利判據等。瑞利首先對氣體密度進行精確測定,並導致了新的惰性氣體氬的發現。這一發現使得瑞利和蘇格蘭化學家拉姆塞 (William Ramsay, 1852—1916) 在1904年分別獲得諾貝爾物理學獎和化學獎。瑞利的工作對於量子論和相對論的誕生也有貢獻。瑞利基於統計物理學導出熱輻射公式即瑞利-金斯 (James Hopwood Jeans, 1877—1946) 公式,表明長波區域輻射能量密度與絕對温度成正比,該公式在短波區域內與實驗不符,揭示了經典物理學的內在困難,對近代物理學的發展起到重要的推動作用。他所分析的天文像差對發光以太理論的影響,傾向於支持靜止以太假説, 但他總體上有些保守的風格阻礙了他直接走向相對論。
瑞利似乎是最後一代紳士科學家。他們生活優渥,出於興趣而投身於科學研究,但並不以此為謀生手段。瑞利也有科學之外的廣泛興趣,如攝影、遠足、小説閲讀等,去世時他正在閲讀小説《愛瑪》。他的論文集題記所選用的雙關語體現了他那種英國紳士的幽默感。題記出自《舊約•詩篇》, 據和合本翻譯為“耶和華的作為本為大,凡喜愛的都必考察。” 其中前半句欽定英文版是“The works of the Lord are great”,從字面上也可以理解為“那位勳爵的工作偉大”,瑞利本人被尊稱為勳爵。瑞利的學術研究風格是廣博、精深和嚴謹,既善於用簡單的設備進行實驗獲取關鍵性數據,又善於發展或應用最適合的數學方法解答特定的物理問題。
對振動理論的開創性貢獻
瑞利在物理學的多個研究領域都有重要工作,對振動理論更是有開創性貢獻。這些貢獻可以概括為線性振動一般理論、模態近似計算方法、振動梁模型改進、自激振動、參激振動和攝動方法六個方面。
 瑞利還指出但沒有展開説明,這個理論可以應用於模態的近似計算。第二個結果是提出了現在所稱的瑞利耗散函數,用於描述振動系統的黏性阻尼;還説明一般情況下,黏性阻尼的存在影響振動方程的解耦,並給出阻尼不影響解耦的一個充分條件,現在稱滿足該條件的阻尼為瑞利阻尼。第三個結果是把結構的位移互等定理推廣到受簡諧激勵的振動情形,開動力學中互等定理的先河。此外,在1877年出版的專著《聲的理論》[1]119-126中,瑞利用瑞利商得到受約束線性振動系統固有頻率的上下限。
瑞利還指出但沒有展開説明,這個理論可以應用於模態的近似計算。第二個結果是提出了現在所稱的瑞利耗散函數,用於描述振動系統的黏性阻尼;還説明一般情況下,黏性阻尼的存在影響振動方程的解耦,並給出阻尼不影響解耦的一個充分條件,現在稱滿足該條件的阻尼為瑞利阻尼。第三個結果是把結構的位移互等定理推廣到受簡諧激勵的振動情形,開動力學中互等定理的先河。此外,在1877年出版的專著《聲的理論》[1]119-126中,瑞利用瑞利商得到受約束線性振動系統固有頻率的上下限。
瑞利對振動理論的重要貢獻是基於瑞利商而發展的模態近似計算方法。1877年,瑞利在《聲的理論》卷I中通過假設第1階振型函數計算瑞利商,作為基頻平方的近似值上限,計算了絃線、杆、梁、膜和板基頻的近似值。這種方法被後人稱為瑞利法。最核心的創見是,瑞利商給出近似值的上限,通過減少瑞利商能夠提高近似的精度。1899年,瑞利在論文《計算振動最嚴重振型的頻率,來自水動力學的例子》[6]407-412中,進一步用該方法計算圓柱形容器中液體晃動的前2階固有頻率。1908年德國理論物理學家裏茲 (Walther Ritz, 1878—1909) 把振動分析轉化為變分問題,通過滿足邊界條件的函數疊加,導出線性代數方程組求解,近似計算了矩形板前幾階固有頻率和振型。1911年,瑞利在論文《關於方形板克拉尼圖形的計算》[8]47-50中明確了裏茨所提出的方法是減小瑞利商的一種便利方法。這種方法被稱為瑞利-里茲法。這種近似求解變分問題的方法也應用於彈性力學計算,仍稱為瑞利-里茲法,是有限元法的基礎。
瑞利在連續體振動方面還有其他貢獻。基礎性的工作是對梁彎曲振動模型的改進。長期以來,梁的彎曲振動都是用歐拉-伯努利梁模型,其中忽略了截面轉動的效應。1877年,瑞利在專著《聲的理論》[1]258-260中,在原來的歐拉-伯努利梁控制方程中增加了反映轉動效應的項。這種修正模型被稱為瑞利梁模型。需要説明的是,1859年,法國數學家和工程師佈雷斯 (Jacques-Antoine-Charles Bresse, 1822—1883) 在《應用力學教程(卷1)》提出相同的方程,比瑞利早18年。瑞利對於杆的徑向振動和薄殼振動也有獨到的見解,改進的處理能與實驗結果更好吻合。
瑞利對於非線性振動理論的發展有原創性貢獻,提出了最早的自激振動理論模型,被稱為瑞利方程。1883年,瑞利在論文《論持續振動》[4]188-193中研究了持續振動的三種產生機制。除了當時已經清楚的受迫振動外,有一種是由風、熱、摩擦等非振盪性激勵產生的週期性持續運動,就是後來所稱的自激振動。瑞利考慮了一種最基本的非線性阻尼,導出了現在所稱的瑞利方程:
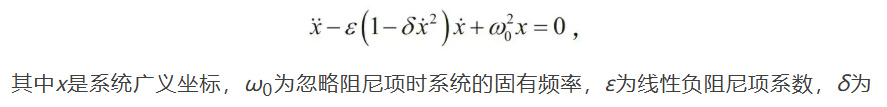 非線性阻尼項與線性阻尼項係數比。瑞利還用諧波平衡法得到了該方程的持續週期運動的幅值。1920年,荷蘭物理學家範德波爾 (B. van der Pol) 不知道瑞利的工作,獨立導出描述三極管振盪的方程,即現在所稱的範德波爾方程,是描述自激振動的典型方程。
非線性阻尼項與線性阻尼項係數比。瑞利還用諧波平衡法得到了該方程的持續週期運動的幅值。1920年,荷蘭物理學家範德波爾 (B. van der Pol) 不知道瑞利的工作,獨立導出描述三極管振盪的方程,即現在所稱的範德波爾方程,是描述自激振動的典型方程。
瑞利是參激振動的早期研究者。在前述《論持續振動》[4]188-193 論文中,瑞利指出能產生持續振動的另一種機制是參數週期性變化,就是現在所稱的參數振動。瑞利給出的描述參數振動的方程,與1868年法國數學家馬蒂厄 (Émile Léonard Mathieu, 1835—1890) 建立的參激振動方程相比, 增加了阻尼項,因此馬蒂厄導出的超幾何函數解不再適用。瑞利似乎不知道馬蒂厄的相關工作,用諧波分析得到以激勵週期2倍為週期的持續振動。這一結果可以解釋1831年法拉第 (Michael Faraday, 1791—1867) 的鉛垂簡諧振動充液容器實驗和1860年德國物理學家麥爾德 (Franz Emil Melde, 1832—1901) 張緊在音叉上弦線振動橫向振動實驗的結果。1883年,瑞利在論文《在振動支撐上液體的捲曲》[4]212-219中進行了實驗研究,結果與理論分析一致。1887年,瑞利進一步研究了雙頻參數激勵的情形[5]1-15,這時他已經知道美國數學家希爾 (George William Hill, 1838—1914) 關於參激振動的工作。
瑞利是振動分析攝動方法的先驅之一。在專著《聲的理論》[1]115-118 中,作為變密度絃線的特例,瑞利研究帶有小集中質量絃線的振動。基於無集中質量絃線的振動特性,把基頻表達為質量比的冪級數。這種基於已知系統分析受到小擾動系統的思想,在1926年被諾貝爾物理學獎獲得者薛定諤 (Erwin Schrödinger, 1887—1961) 應用於量子力學而形成瑞利-薛定諤微擾理論。此外,瑞利晚期工作中還有攝動分析重要技巧如匹配過程和重整化的雛形。例如:1912年《論波通過分層介質的傳播》[8]71-90研究了波在轉換層全反射的不同漸近展開中的常數匹配;1917年《論光在規則分層介質的反射》[8]492-503對薄層首次散射的展開式重新定義指數式並求和,使之對多個薄層有效。
奠定振動理論體系的《聲的理論》
1871年瑞利結婚後,風濕熱嚴重發作影響他的健康。醫生建議他到埃及旅行作為康復治療,於是這對新婚夫妻在1872年下半年到埃及,乘房船在尼羅河上觀光。正是在這次旅行中,瑞利開始寫那部尚無先例的專著,對振動和聲音相關的實驗發現進行系統的數學論述。他每天上午都在船艙中寫作,一直到1873年春天返回英國。回國後瑞利在自己的莊園中繼續進行該書的寫作。他共用5年時間,完成千餘頁的鉅著《聲的理論》。上卷論述作為聲學基礎的振動理論,於1877年出版;下卷論述聲波傳播,於1878年出版。兩卷分別於1894和1896年修訂擴充再版,1926年、1929年和1937年3次重印。1945年在美國出版了兩卷合訂本,隨後多次重印。《聲的理論》至今仍被廣為引用,堪稱經典。其中有過半的篇幅 (包括第1卷全部) 是關於振動的闡述,所形成的振動理論體系,被後來的眾多振動著述沿用。
《聲的理論》中的振動理論可以分為三部分,離散系統振動、連續系統振動以及與聲學相關的振動專題。離散系統振動為基礎,包括簡諧運動以及單自由度、多自由度系統的特性和響應。連續系統振動是振動理論的主體,有詳細的闡述,包括絃線的橫向振動、杆的徑向振動和扭轉轉動、梁的彎曲振動、膜的振動、板的振動、殼的振動,以及第2卷中的三維固體振動。與聲學有關的振動專題性內容,第1卷中有電振盪,第2卷中有空氣的振動、管道中的振動、矩形房間中的空氣振動等,這類振動問題與聲的傳播密切相關。絕大部分內容為線性振動,但也涉及單自由度的非線性振動。前兩部分內容,即離散和連續系統振動,有廣泛影響,是隨後的振動專著和教材的核心內容。
《聲的理論》是第一部數理聲學專著,集聲學理論之大成, 系統總結了直到著作出版時的300餘年重要成果,其中有歐拉 (Leonhard Euler, 1707—1783)、達朗貝爾 (Jean le Rond d’Alembert, 1717—1783)、拉格朗日 (Joseph- Louis Lagrange, 1736—1813) 等大師的經典成果,也有作者瑞利的貢獻。瑞利的研究成果多數已經以論文形式發表,例如單自由度阻尼系統的自激振動和參激振動、多自由度離散振動的一般理論、殼的振動等。除這些內容被整合入專著之外,也有少量在書中首次發表的新結果,例如約束對振動系統頻率的影響、梁的彎曲振動中剪切效應建模和分析,在第2版中增加了帶集中質量絃線振動的攝動分析。
就振動理論的發展而言,《聲的理論》的重要意義是奠定了學科發展的基礎。該書總結了振動問題研究的所有成果,形成了統一的理論體系。在線性振動的範疇內,這一理論體系沿用至今。除了從單自由度到有限多自由度再到無窮多自由度連續體的展開方式外,更重要的是該書有一以貫之的方法論。在力學方面,強調廣義座標與廣義力的應用,系統地採用拉格朗日方程。在分析方法方面,諧波分析系統地應用於線性受迫振動和參激振動的響應分析,也用於非線性受迫振動和自激振動的響應分析。諧波分析不僅是求解線性振動問題的利器,也是後來研究非線性振動的重要方法之一。雖然諧波分析的數學基礎由法國數學家傅里葉 (Baron Jean Baptiste Joseph Fourier, 1768—1830) 在1822年奠定,但其系統地應用於振動分析開始於瑞利的工作。
《聲的理論》的重要意義還在於開闢了振動理論發展的道路。經典振動理論的現代發展肇始於複雜振動系統固有頻率的近似計算。固有頻率近似計算的主要理論基礎是瑞利方法及其發展。該書系統地使用瑞利方法確定連續體的振動基頻,開固有頻率近似計算的先河。線性振動理論成熟之後,非線性振動是振動理論重要的知識生長點。該書不僅有含平方非線性剛度項系統的受迫振動和有立方非線性阻尼項系統的自激振動的理論性工作,而且有預見性地猜測後來所稱的輸電線舞動是自激振動 (第2版增加的內容)。作者提到絃線在風載荷作用下在垂直於風的方向振動,並斷言科學解釋需要尚沒有的氣動力理論。40年後,鄧哈託 (Jacob Pieter Den Hartog, 1901—1989) 在普朗特 (Ludwig Prandtl, 1875—1953) 氣動力理論基礎上明確了輸電線舞動的機理是自激振動。
《聲的理論》既系統總結了已知成果,又有預見性地引領未來發展,是部承先啓後、繼往開來的奠基性著作,廣泛有效地傳播了振動理論,對於學科發展起了不可替代的重要作用。
美國三院院士克蘭德爾 (Stephen H. Crandall, 1920—2013) 在1988年評價《聲的理論》, “為振動教學樹立榜樣超過一個世紀,……過去50年來出現的大多數工程師振動教科書都可以被視為試圖向大學生解釋瑞利的想法。”[11]
瑞利曾觀察到,科學史上的很多發現,當時很少引起人們注意,但後來這些發現猶如種子,向下紮根,向上結果。瑞利在振動理論中的發現如自激振動和攝動方法就是這樣。瑞利撰寫的專著《聲的理論》極大地促進了振動理論的傳播。這也印證了弗朗西斯•培根的名言,“知識的力量,不僅取決於其自身價值,更取決於它是否能被傳播,以及被傳播的深度和廣度。”瑞利對振動理論的開拓性貢獻,既包括創新性成果,也包括有效的傳播。
參考文獻
[1] STRUTT J W. The theory of sound (Vol. 1) [M]. 2nd ed. London: MacMillan, 1894.
[2] STRUTT J W. The theory of sound (Vol. 2) [M]. 2nd ed. London: MacMillan, 1896.
[3] STRUTT J W. Scientific papers (Vol. 1) [M]. Cambridge, UK: Cambridge University Press, 1899.
[4] STRUTT J W. Scientific papers (Vol. 2) [M]. Cambridge, UK: Cambridge University Press, 1900.
[5] STRUTT J W. Scientific papers (Vol. 3) [M]. Cambridge, UK: Cambridge University Press, 1902.
[6] STRUTT J W. Scientific papers (Vol. 4) [M]. Cambridge, UK: Cambridge University Press, 1903.
[7] STRUTT J W. Scientific papers (Vol. 5) [M]. Cambridge, UK: Cambridge University Press, 1912.
[8] STRUTT J W. Scientific papers (Vol. 6) [M]. Cambridge, UK: Cambridge University Press, 1920.
[9] STRUTT R J. Life of John William Strutt, third Baron Rayleigh [M]. London: D. Edward Aronld, 1924.
[10] LINDSAY R B. Lord Rayleigh — The man and his work [M]. London: Pergamon Press, 1970.
[11] CRANDALL S H. Rayleigh’s influence on engineering vibration theory [J]. Journal of Acoustics Society of America, 1998, 83(S1): 43-44
本文經授權轉載自微信公眾號“自然擷英”。
 特 別 提 示
特 別 提 示
1. 進入『返樸』微信公眾號底部菜單“精品專欄“,可查閲不同主題系列科普文章。
2. 『返樸』提供按月檢索文章功能。關注公眾號,回覆四位數組成的年份+月份,如“1903”,可獲取2019年3月的文章索引,以此類推。