量子場論中的最大糾纏假設_風聞

量子糾纏以及量子信息中的有關概念被應用於粒子物理學，引發了相關學界的關注，本文將介紹其中一些具有啓發性的研究結果。

撰文 | 付海龍（中國科學院理論物理研究所20級博士研究生）

2025年是量子力學建立100週年，量子力學與經典物理相區別的一項重要特點是量子糾纏(quantum entanglement)。對於一個由兩個子系統組成的複合量子系統，假如子系統的完備

當這個疊加態的波函數無法分解為直積的形式時，就稱之為糾纏態(entangled state)。在量子力學提出後，量子糾纏的現象就已經被意識到[1]，歷史上關於EPR佯謬和量子糾纏的討論極大地推動了量子力學的發展。時至今日，對量子糾纏以及量子力學的理論基礎的相關研究仍然是一個正在蓬勃發展的領域，關於量子糾纏以及其他刻畫量子系統之間關聯的現象的研究被稱為量子信息科學。

隨着近些年來量子計算技術與量子信息學科的快速發展，量子糾纏以及量子信息中的有關概念在粒子物理學中的應用引發了一些關注，本文將介紹其中一些具有啓發性的研究結果。

1 電弱相互作用中的最大糾纏

1.1 QED過程中的糾纏產生

量子電動力學(QED)是電磁相互作用的基本理論，它描述光與物質相互作用，小到微觀粒子，大到宏觀物體之間的電磁力都由QED決定。因此一個重要的問題是量子糾纏是如何在QED中體現的，以及QED到底可以產生多大程度糾纏，產生的這些糾纏是否足以破壞貝爾不等式從而體現出QED作為量子理論的特性？為了回答這個問題，首先要説明如何定量地刻畫量子糾纏。兩個電子組成的系統，可以看作是一個雙量子比特體系，其中每個電子可以是右手和左手的螺旋度本徵態，因此可以將兩個電子的總系統表述為螺旋度本徵態直積態

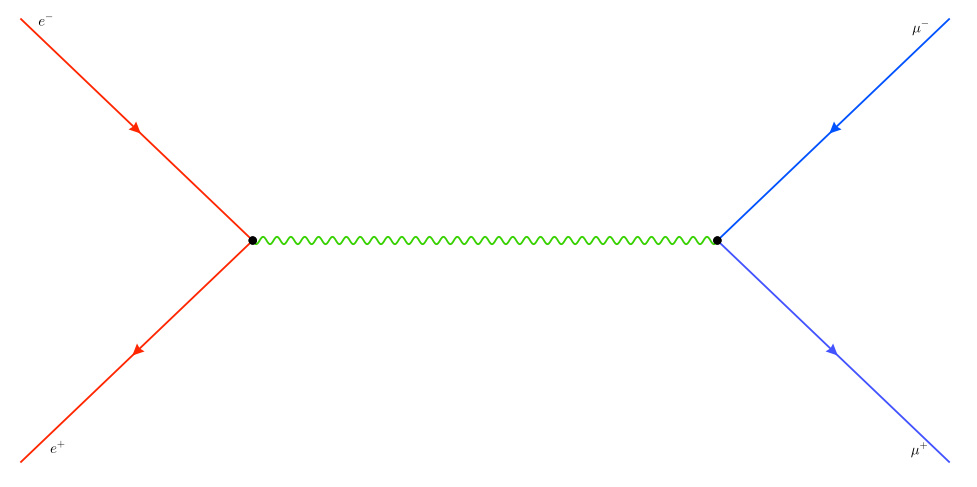從初態正負電子對到末態正負μ子對的費曼圖

其中一對正負電子通過交換一個虛光子到末態的正負子對。通過量子場論的標準方法可以計

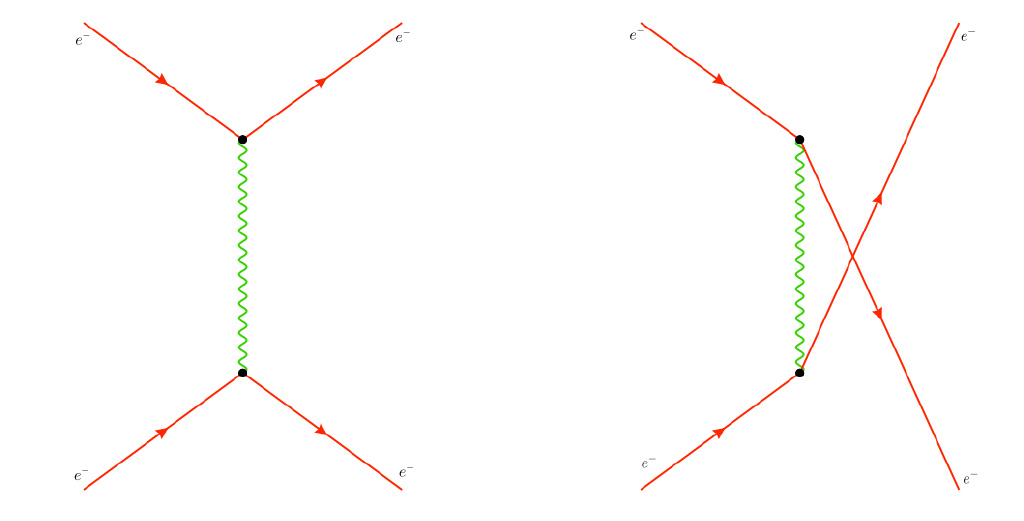正負電子彈性散射的QED過程

由於兩個電子是全同粒子，該過程包括t道（左）與u道（右）的貢獻。

事實上在低能極限下，可以發現電子電子之間無論螺旋度如何組合，都可以達到最大糾纏，這正説明在低能下可以較容易地製備出糾纏電子對。

1.2 電弱理論中的最大糾纏假設

上述分析説明，QED作為電磁相互作用的基本理論可以產生量子糾纏，並且可以達到最大糾纏，也就是實現了對貝爾不等式最大程度的破壞，反映了這一基本相互作用的量子特性。如果從另一個角度看待這一問題，可以考慮將量子理論的糾纏特性作為一個更基本的假設，從這一假設出發，研究是有可能導出對基本相互作用的某些約束。

首先考慮QED，放寬對其理論形式的限制，將電子光子的耦合頂點表示為：

項自然破壞了規範對稱性，不描述真實世界中的電動力學。但是如果我們將可以產生最大程度的糾纏作為一項基本相互作用的性質來對其施加約束，將會得到對稱性更高的解[2]。對這一可能性進行分析，通過計算該理論中各種基本QED過程的併發度，並且要求它們可以取到最大值，可以得到這樣一組解：

2 深度非彈性散射中的最大糾纏假設

對於強相互作用，也存在類似的現象。高能標下的強子結構由部分子模型描述，例如在高能輕子與核子的深度非彈性散射實驗中，發現高能標下的核子內部具有類點狀的部分子結構，這些

將質子作為一個整體的量子態來考慮，它本身是一個純態。但是在深度非彈性散射實驗當中，通過高能量探針對其進行探測，只能探測到其中的一小部分，這實質上是進行了一次量子測量，因此被探針探測到的這一部分與未探測到的這一部分將產生量子糾纏。在一個測量過程中，儘管總系統是純態，但其中一個子系統的約化密度矩陣將不再描述純態，使得它與總系統中的其他部分產生非0的糾纏熵。深度非彈性散射過程中質子系統的糾纏熵可以表示為：

由於此處糾纏熵的定義與部分子的個數有關，在高能對撞機上，由同一個初態部分子演化出的末態強子的個數對應的多重數分佈(multiplicity distribution)可以測量，這一物理量與糾纏熵能夠產生直接的聯繫，因此可以基於最大糾纏的假設來計算高能標強子化過程中的糾纏熵，並將其與強子結構函數聯繫起來。近年來，這一方法被用到高能強子結構的研究中，取得了一些有意思的結果[5-7]。

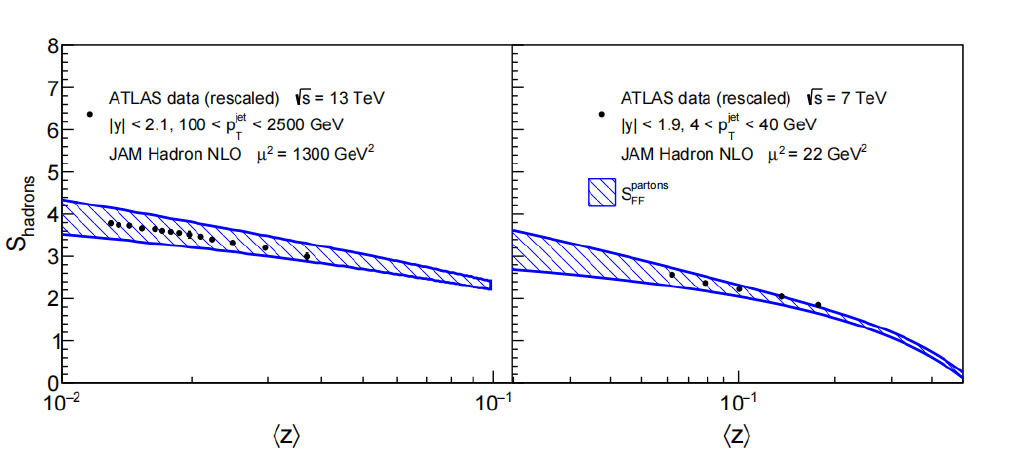最大糾纏方法給出的理論預言與ATLAS實驗數據的比較[7]

總結

最大糾纏假設將量子信息理論中的概念應用到高能物理研究中，近年來相關的方法被得到了一些關注，在這一假設下可以給出一些有趣的結果，其背後是否藴含更深刻的原理仍然有待發掘。

參考文獻

[1] EINSTEIN A, PODOLSKY B, ROSEN N. Can quantum-mechanical description of physical reality be considered complete?[J/OL]. Phys. Rev., 1935, 47: 777-780. DOI: 10.1103/PhysRev.47.777.

[2] CERVERA-LIERTA A, LATORRE J I, ROJO J, et al. Maximal Entanglement in High Energy Physics[J/OL]. SciPost Phys., 2017, 3(5): 036. DOI: 10.21468/SciPostPhys.3.5.036.

[3] KHARZEEV D E, LEVIN E M. Deep inelastic scattering as a probe of entanglement[J/OL]. Phys. Rev. D, 2017, 95(11): 114008. DOI: 10.1103/PhysRevD.95.114008.

[4] KOVCHEGOV Y V, LEVIN E. Quantum Chromodynamics at High Energy: Vol. 33[M/OL]. Oxford University Press, 2013. DOI: 10.1017/9781009291446.

[5] TU Z, KHARZEEV D E, ULLRICH T. Einstein-Podolsky-Rosen Paradox and Quantum Entanglement at Subnucleonic Scales[J/OL]. Phys. Rev. Lett., 2020, 124(6): 062001. DOI: 10.1103/PhysRevLett.124.062001.

[6] HENTSCHINSKI M, KHARZEEV D E, KUTAK K, et al. QCD evolution of entanglement entropy[J/OL]. Rept.Prog. Phys., 2024, 87(12): 120501. DOI: 10.1088/1361-6633/ad910b.

[7] DATTA J, DESHPANDE A, KHARZEEV D E, et al. Entanglement as a Probe of Hadronization[J/OL]. Phys.Rev. Lett., 2025, 134(11): 111902. DOI: 10.1103/PhysRevLett.134.111902.

本文經授權轉載自微信公眾號“中國科學院理論物理研究所”。

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。