蓋爾曼：複雜性是什麼？_風聞

本文以討論複雜性的度量為主線，貫穿了對有效複雜性、規律、複雜適應系統、複雜性的本質與演化等議題的思考。諾獎得主、研究複雜系統的聖塔菲研究所聯合創始人之一的美國物理學家蓋爾曼認為，較高的有效複雜性存在於既非全然有序又非全然無序的事物中。研究對象的有效複雜性可用其所具規律的簡潔描述的算法信息量來度量。其中，規律可用計算互算法信息量的方法求得。而複雜適應系統（如生物或生成策略的計算機程序）則決定了研究對象的哪些規律需要被識別。宇宙的基本規律和初始條件都相對簡單，有效複雜性主要來源於量子力學所引入的不確定性以及經典物理中混沌現象所帶來的不確定性。自組織機制將一些偶然事件轉化為“凍結的偶然事件”，而後者會在宇宙的某個粗粒化歷史的各部分或各方面之間產生大量的互算法信息，從而形成規律。我們的宇宙從誕生以來，複雜性的外延一直在擴展，但在遙遠的未來，複雜性的範圍終將萎縮。

撰文 | Murray Gell-Mann

翻譯 | 許寧、羅翠

審校 | 錢嘉欣

論文題目：What is Complexity?

論文地址：https://complexity.martinsewell.com/Gell95.pdf

複雜性是什麼？已有許多的量被提出用於作為諸如複雜性這樣的概念的度量。事實上，要全面涵蓋我們對於複雜性及其對立面——簡單性的所有直觀想法，需要多元化的度量。

有些量屬於時間（或空間）的度量範疇，例如計算複雜度。這些量關心一台標準通用計算機執行特定任務所需的最短時間（或最小存儲空間）。計算複雜度本身即與完成特定計算所需的最少時間（或運行步數）直接相關。

其它被提議的量則屬於信息度量範疇，大體而言，它們特指傳遞特定信息所需的最短消息長度。例如，一個比特串的算法信息量（AIC，algorithmic information content）被定義為使標準通用計算機輸出該比特串然後停止運行的最短程序的長度。

所有這樣的量，在用於度量現實世界實體的複雜性時，在某種程度上都具有語境相關性甚至主觀性。它們依賴對實體的描述的粗粒化程度（即細節的層級）、所假定的對世界已有的知識和理解、使用的語言、從該語言轉換為比特串的編碼方法，以及對特定理想計算機標準的選擇。然而，若研究者考察一系列規模與複雜性遞增的相似實體，且僅對規模增大時的度量變化感興趣，那麼很多隨機特徵自然可以忽略不計。計算複雜度的研究者通常關注當問題規模不斷增大時，其求解時間是否隨着問題規模的增大呈多項式（而非指數甚或更糟糕的形式）遞增。可以説，任何對複雜性的度量最好的用武之地是去比較那些至少有一方在該度量下具有高複雜性的事物。

許多備選量是不可計算的。例如，一個長比特串的AIC很容易被判斷為小於或等於某個值。但對任意一個這樣的值，都無法排除AIC因該字符串所隱藏的規律（regularity）被某個尚未發現的定理揭示，從而降到更低的可能性。一個不可壓縮比特串則不存在這種規律。這樣的比特串被定義為“隨機比特串”。一個給定長度的隨機比特串擁有最大的AIC，因為能讓標準計算機輸出它後停止的最短程序，只是一條在該字符串之前加上“PRINT”的指令。

AIC的這種特性，有時也被稱為“算法隨機性”。這種特性導致其並不適合作為複雜性的度量，否則莎士比亞作品反而比諺語中“由一屋子猴子”隨機敲出的相同長度的亂碼具有更低的AIC。

能夠更好地反映日常對話和科學論述中所提及的“複雜性”的度量，並不是對實體最簡描述的長度（大致如同AIC），而是對該實體的規律的集合的簡潔描述的長度。因此，一個幾乎完全隨機、不具備規律的事物，其有效複雜性（effective complexity）接近於零；而一個完全規律的事物，例如一條全由0組成的比特串，其有效複雜性同樣也接近於零。只有在完全有序和完全無序之間的中間地帶，才存在較高的有效複雜性。

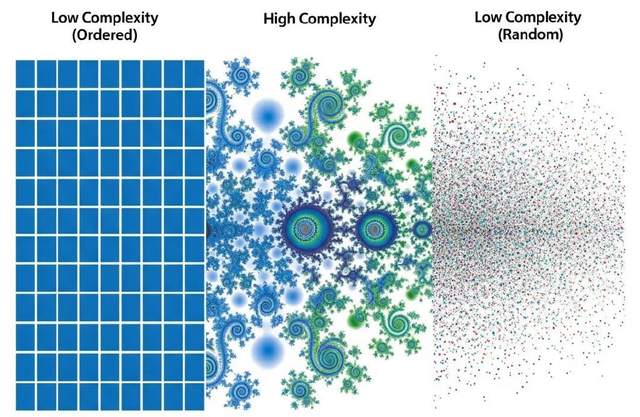“只有在完全有序和完全無序之間的中間地帶，才存在較高的有效複雜性”（圖片由AI生成）

沒有任何程序可以找出關於實體的所有規律，但這些規律的類別能被識別。發現規律的過程如下：在獲取關於實體的可用數據後，將其處理成如比特串的某種形式，然後以特定方式將該串分割成若干部分，並尋找各部分間的互算法信息量（mutural AIC）。例如對於一個被分成兩部分的比特串，它的互算法信息量即為各部分AIC之和減去整體的AIC所得的差。超過特定閾值的AIC可被視為出現規律的判定依據。對於已識別的規律，對其所作的描述的AIC即為與之對應的有效複雜性。更準確地説，任何特定的規律都可以被視為將所研究的實體嵌入一個共享這些規律、僅在其他方面有所差異的實體集合中。通常，這些規律會為集合中的每個實體賦予一個概率。（在許多情況下，各實體的概率相同，但不排除實體間概率相異的情況出現。）這些規律的有效複雜性則可定義為描述該實體集合及其概率分佈的AIC。（如需詳述特定實體，如原始實體，則需要額外信息。）

一些作者試圖通過互算法信息(mutual algorithmic information)，而非相應規律的簡潔描述的長度來刻畫複雜性。然而，這種度量的選擇與“複雜性”的一般含義並不怎麼相符。舉一個簡單的例子，任何一個完全由00對和11對組成的比特串，都有着一個顯而易見並能用非常簡短的方式進行描述的規律，即由奇數位組成的序列與由偶數位組成的序列完全相同。然而，對於一個長比特串而言，這些序列之間的互算法信息量是巨大的。顯然，這種情況下，用簡短描述的長度來表徵複雜性，比用互算法信息量之多寡來表示更為恰當。

既然不可能找出某一實體的所有規律，那麼問題就出現了：由誰或由什麼來決定哪些類別的規律需要被識別？答案之一指向一類極其重要的系統，其中的每一個系統都在識別到達它的數據流中的特定規律，並將這些規律壓縮成一個簡潔的信息集。數據流包含了關於系統自身、其所處環境、以及環境與系統行為之間相互作用的信息。這個信息集或“圖式（schema）”會經歷變化，不同圖式之間還會存在競爭。每個圖式都可以與部分數據一起被用於描述系統及其所處的環境、預測未來以及為系統設定行為規範。但這種描述和預測可以與更多數據進行比對檢驗，對比後的反饋會影響圖式之間的競爭。同樣，符合規範的行為會對現實世界產生實際影響，因而這也會影響競爭。通過這種方式，圖式不斷演化。其演化總體趨向於作出更好的描述和預測，以及或多或少地順應現實世界的選擇壓力。

複雜適應系統（complex adaptive systems）在地球上運作的實例包括：生物進化、動物（包括人類）的學習與思考、哺乳動物及其他脊椎動物的免疫系統功能、人類科學事業的運作、以及那些被設計或編程以生成策略（例如通過神經網絡或遺傳算法）的計算機的行為。顯然，複雜適應系統具有催生其他複雜適應系統的傾向。

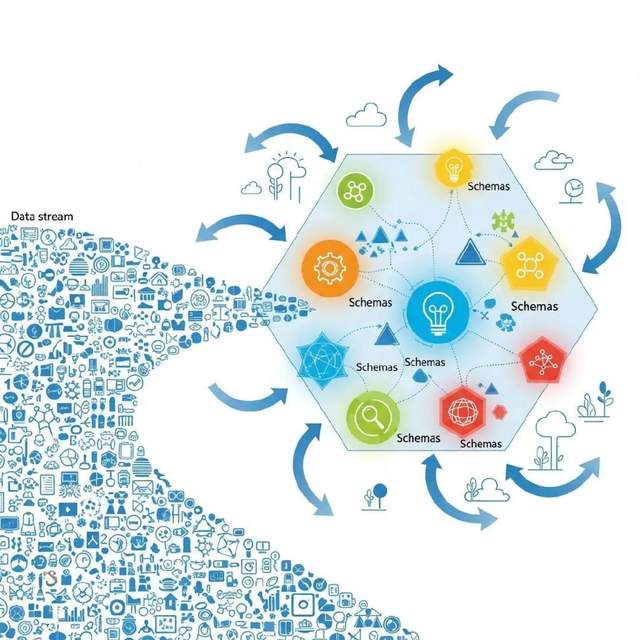複雜適應系統與環境數據交互，生成圖式（圖片由AI生成）

值得向本刊讀者説明的是，例如約翰·霍蘭（John Holland）就使用了一套不同的術語來描述一些相同的想法。他用“適應主體（adaptive agent）”來指稱上面定義的複雜自適應系統，而用“複雜適應系統”來指稱由許多可對彼此行為做出預測的自適應主體組成的複合複雜適應系統（composite complex adaptive system）（如經濟或生態系統）。我所説的圖式，他稱為本質模型（internal model）。我們倆都遵從一句老話：科學家寧可用別人的牙刷，也不會用另一位科學家提倡的術語。

當然，任何複雜適應系統在發現規律時都可能犯錯。容易迷信、並且經常否認顯而易見的事物的我們（人類）對這類錯誤再熟悉不過了。

除了出錯的可能性，我們還應考慮計算難度。從一個高度壓縮的圖式（例如一個科學理論）和一些特定的附加數據（例如邊界條件）中推導出實際的預測結果，需要花費多少時間？在這裏，我們就遇到了“複雜性”的時間度量。以邏輯深度為例。對於一個比特串來説，邏輯深度（logical depth）與用標準通用計算機計算該比特串、將其打印出來並停止運行所需的時間有關。這個時間通過對能夠完成該任務的各種程序求均值得到。求均值時，較短的程序被給予更大的權重。那麼，如果能將實體的適當粗粒化的描述編碼成比特串，我們就可以探討任何實體的邏輯深度。

邏輯深度的一個逆向概念是隱秘度（crypticity），它衡量的是計算機從比特串反推生成它的較短程序之一所需的時間。在人類的科學事業中，我們可以將隱秘度大致理解為從一組數據中構建一個好理論的難度，而邏輯深度則是對從理論出發進行預測的難度的粗略衡量。

通常很難判斷一個看起來複雜的事物是真正具有很高的有效複雜性，還是僅僅反映其內在的簡單性以及一定程度的邏輯深度的組合。例如，當我們看到曼德爾布羅特著名的分形集的一個相當詳細的圖案時，在我們瞭解到它其實可以通過一個非常簡單的公式生成之前，我們可能會認為它具有很高的有效複雜性。

它具有的是（甚至並不巨大的）邏輯深度而非有效複雜性。在思考自然現象時，我們經常需要區分有效複雜性和邏輯深度。例如，原子核能級的看似複雜的模式可能很容易被錯誤地歸因於基本層面上的某種複雜定律，但現在人們相信它遵循一個關於夸克、膠子和光子的簡單的基礎理論，儘管需要大量的計算才能從基本方程推導出其詳細模式。因此，這種模式具有相當大的邏輯深度，而有效複雜性卻非常低。

現在看來，宇宙中所有物質行為的基本規律，即所有基本粒子及其相互作用的統一量子場論，很可能是非常簡單的。(事實上，我們已經有了超弦理論這個貌似合理的候選理論。）同樣，描述宇宙在其膨脹之初的初始狀態的邊界條件可能也很簡單。如果這兩個命題都是真的，那麼是否意味着宇宙中幾乎不存在任何有效複雜性？完全不是，因為偶然性在持續不斷地起作用。

即便給定了基本規律和初始條件，宇宙的歷史也絕非註定。因為這規律是量子力學的，它只能給出各種歷史版本的概率。此外，歷史只有被充分地粗粒化以顯示退相干時（即它們之間沒有干涉項）才能被賦予概率值。因此，量子力學帶來了大量不確定性，遠遠超出與海森堡不確定性原理相關的、微不足道的不確定性。

當然，在許多情況下，量子力學概率非常接近確定性，因此確定性的經典物理學是一個很好的近似。但即便在經典條件下，即使規律和初始條件都被精確指定，不確定性仍然可能因為對先前歷史的無知而被引入。進而，這種無知的影響可能會被非線性動力學中的混沌現象所放大。在混沌現象中，未來的結果對當前條件的微小變化極其敏感。

我們可以將宇宙可能存在的各種粗粒化歷史想象為形成一顆具有分支的樹，每個分支都有相應的概率。注意這些是先驗概率（priori probability）而非統計概率（statistical probability），除非我們將我們的宇宙視為由許多宇宙構成的巨大集合中的一員，從而形成一個"多重宇宙"。當然，即使在單一宇宙中，也會出現可重複事件（如物理實驗）。對於這些事件，這個宇宙的量子力學的先驗概率會產生傳統的統計概率。

我們周圍世界中的任何實體，例如每個人類個體，其存在不僅依賴於簡單的基本物理定律和早期宇宙的邊界條件，也取決於一連串長得不可思議的概率性事件的結果，而其中每一個事件原本都可能以不同的方式發生。

現在，許多偶然事件，例如氣體中某個特定分子在分子碰撞中向右而非向左反彈，在絕大多數情況下對未來的粗粒化歷史幾乎沒有什麼影響。然而，有時一個偶然事件可能會對未來產生廣泛的影響，儘管這些影響通常侷限於特定的時空區域。這種“凍結的偶然事件（frozen accident）”會在宇宙的某個未來的粗粒化歷史的各個部分或各方面之間產生大量的互算法信息，對於許多此類歷史及其各種劃分方式也是如此。

但是，這種產生大量互算法信息的情況，與我們已説到的規律完全相符。因此，隨着宇宙歷史中時間的推移以及事件（伴隨着各種結果的概率）的不斷積累，凍結的偶然事件也隨之積累，從而產生規律。

宇宙的大部分有效複雜性體現在對那些凍結的偶然事件及其後果的描述的AIC，而只有一小部分來自宇宙的簡單的基本定律（基本粒子定律和膨脹開始時的條件）。當然，對於宇宙中的給定實體而言，只有那些造成其自身規律的凍結的偶然事件，才會與基本定律一起，對其有效複雜性有貢獻。

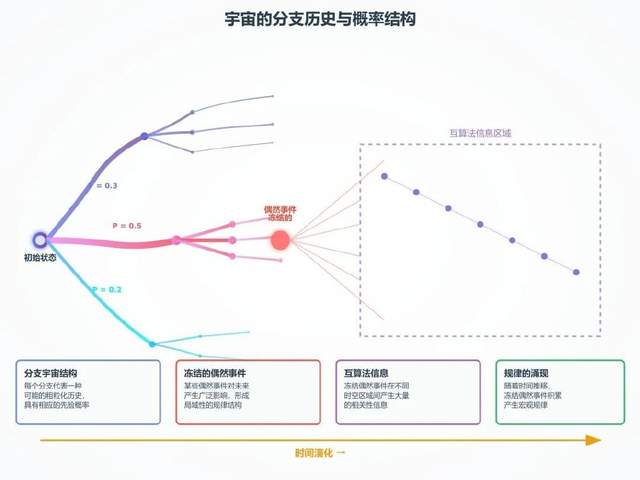宇宙的分支歷史與凍結的偶然事件示意圖（圖片由AI生成）

隨着宇宙變得更加古老，凍結的偶然事件不斷堆積，使有效複雜性增加的機會也持續積累。因此，複雜性外延呈擴張趨勢，儘管任何給定實體在給定時間段內其複雜性都可能增加或減少。

越來越複雜形式的出現並不是一個僅在複雜適應系統演化中才能見到的現象，儘管對於複雜適應系統而言，在某些特定情況下，增加複雜性可能會帶來演化優勢。

熱力學第二定律要求平均熵（或無序度）增加，但這並不妨礙局部的有序通過各種自組織機制產生。這些機制能將偶然事件轉變為其凍結狀態，從而產生大量的規律。同樣，這類機制也並非僅限於複雜適應系統。

不同的實體在發展出更高複雜性方面可能具有不同的潛力。目前在有效複雜性方面與同類事物沒有顯著區別的某些事物，卻會因其未來可能達到的複雜性而變得引人注目。

因此，定義一個新的量——“潛在複雜性（potential complexity）”，作為未來時間的函數至關重要。對未來時間的定義取決於其相對的固定時刻（比如現在）。這個新的量表示實體在未來某時刻的有效複雜性，它是通過對宇宙在現在到未來那個時刻之間的各種粗粒化歷史進行加權平均得到。

越來越多複雜形式隨着時間推移不斷出現的時代可能不會永遠持續下去。在極其遙遠的未來，如果宇宙中幾乎所有原子核都衰變為電子和正電子、中微子和反中微子以及光子，那麼以界限分明的個體為特徵的時代可能會走向終結。同時，自組織變得稀有，複雜性的範圍也會開始萎縮。

作者簡介

莫里·蓋爾曼（Murray Gell-Mann，1929—2019），美國物理學家，1964年提出夸克模型，被譽為“夸克之父”，1969年因其對亞原子粒子的分類及相互作用的研究獲諾貝爾物理學獎。1984年，蓋爾曼成為聖塔菲研究所的聯合發起人之一。他在1994年的短文《Let’s Call It Plectics》中闡述了聖塔菲研究所的學科方向，之後在1995年出版的著作《夸克和美洲豹》中全面展示了其對基本物理規律與生命湧現現象之間的關係的思考。

本文經授權轉載自微信公眾號“集智俱樂部”，編輯：趙思怡，原標題為《有效複雜性的邊界：在有序與無序之間》。

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。