方程、曲面、時空與超越：龐加萊受希爾伯特之邀的跨領域航行_風聞

譯者按：1909年4月，龐加萊受希爾伯特（Hilbert）之邀，在沃爾夫斯凱爾基金會（Wolfskehl-Stiftung）贊助下（希爾伯特時任該基金委員會主席），在哥廷根進行了一系列講座，這也是首屆沃爾夫斯凱爾講座。講座的主要內容後被收入《關於純粹數學和數理物理學中選定課題的六次講座》（Sechs Vorträge über ausgewählte Gegenstände aus der reinen Mathematik und mathematischen Physik, Leipzig and Berlin, Teubner, 1910. 8vo. 60 pp）一書。

此文是美國數學家伯克霍夫在1911年對此係列演講合集的書評，對六次講座主題進行了簡要介紹。關於龐加萊受邀演講相關歷史，見本文“譯後記”。

撰文 | G. D. Birkhoff

翻譯 | 金威

原書扉頁書影（本文插圖為譯者所加，下同）。

1909年4月22日至25日，在沃爾夫斯凱爾委員會（Wolfskehl commission）的邀請下，龐加萊（Poincaré）在哥廷根發表了這六次演講，以精湛和富有啓發性的方式論述了一系列有趣的課題。因為本書的性質決定，對方法和結果的概述需要極其簡潔，這使得這本小書讀起來很吃力。幸運的是，讀者如果不滿足於書中提供的簡要論述，還可以參閲龐加萊的近期文章，以補充理解其中的大部分內容。[1]各主題的順序為：(1) 弗雷德霍姆（Fredholm）方程；(2) 積分方程理論在流體運動中的應用；(3) 積分方程理論在赫茲波（Hertzian wave）中的應用；(4) 阿貝爾積分的約化（reduction）和富克斯函數理論；(5) 超限數（transfinite numbers）；(6) 新的力學。第六次演講具有通俗講演的性質，且以法語進行。[2]

1

弗雷德霍姆方程

第二類的積分方程

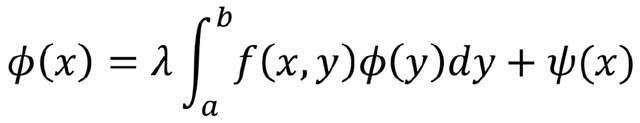
已知存在兩種形式解，其中一種是諾伊曼（Neumann）解，它是參數λ的正整數次冪的冪級數，對λ較小的值收斂；另一種是弗雷德霍姆解，它是λ的兩個整函數的商。龐加萊首先通過組合計數推導出logD(λ)的基本公式，其中D(λ)是弗雷德霍姆預解式（Fredholm resolvent）的分母，然後立即利用預解式的諾伊曼公式定義了分子。通過這種比較方法，可以清晰地分析積分方程的解。該方法的自然推廣使龐加萊能夠處理下列重要情況，即核

存在性；但在他的公式中，分子和分母中仍然保留了一個共同因子，而在這裏通過使用修正的預解式可將其去除。這個解算子可通過從弗雷德霍姆解算子中刪除某些項，以非常簡單的方式獲得。

演講給出了f(x,y)及其所有迭代核變為無窮大時的一些部分結果，最後考慮了屬於第一類的兩個特殊的積分方程[3]，它們通過傅立葉積分和級數可約化為弗雷德霍姆方程。

2

積分方程理論在流體運動中的應用

在本演講和下一演講中，我們將展示典型且重要的例子，説明數學物理問題是如何引出弗雷德霍姆方程的。

第一個問題是在深度變化的海洋中如何確定流體運動，考慮到地球自轉且受週期性攝動力的影響。如果忽略由於水位變化而產生的引力，則會得出一個關於兩個獨立變量的非齊次二階線性偏微分方程，即龐加萊所考慮的方程。若海洋四周是垂直的崖壁，則採用希爾伯特和皮卡（Picard）的方法來構造相關的積分方程的核或格林函數，該方程屬於第一類積分方程。隨後可以通過凱洛格（Kellogg）的方法或由龐加萊提供的複平面積分方法來處理該方程，原方程將轉化為一個等效的第二類方程。

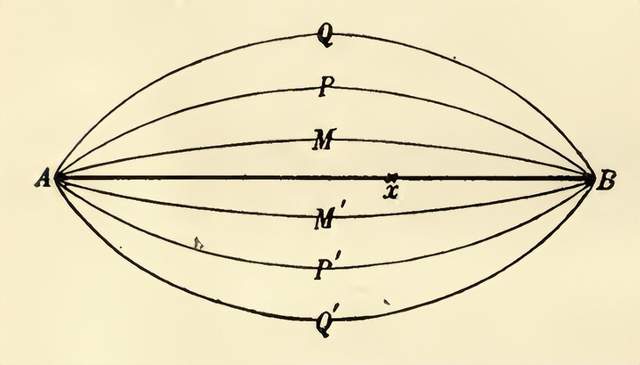
流體運動龐加萊積分方法的示意圖，示積分路徑選取（摘自原書16頁）。

如果海岸線不是垂直的，則相應的邊界是微分方程的一條奇異線（singular line）。此外還需考慮第二條線（臨界緯度，critical latitude）。通過相繼的三個步驟，可以再次實現類似的簡化。因此，證明了在這兩種情況下均存在解。最後指出，如果不忽視由於水位移產生的引力，便不會出現新的困難。

3

將積分方程理論應用於赫茲波

龐加萊揭示了赫茲波[4]在地球表面沿曲線傳播的現象，這也是無線電報信息可以極遠距離發送的原因。這種現象是由於赫茲波的波長遠大於光波的波長，而光波是沿直線傳播的。書中給出了定量的數學討論。通過將地球視為外導體，發射器視為內導體，並考慮阻尼同步振動，我們可以得到一個第二類積分方程，以確定在地球表面產生的電密度μ。

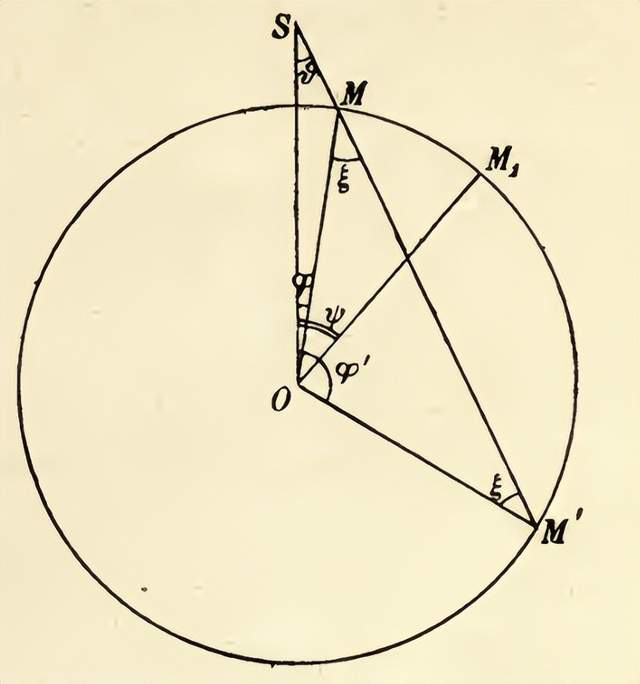
龐加萊對球體表面波傳播的幾何關係分析圖（摘自原書第27頁）。

但這僅僅得出了一個存在定理。龐加萊通過獲得μ的近似表達式，得到了問題的實際結論；該方法取決於勒讓德多項式中μ的展開，以及漸近公式的使用。結果表明，曲率隨着波長的增加和發射器與地球距離的減小而增加。[5]

4

阿貝爾積分的約化與富克斯函數理論

如果一個給定的阿貝爾函數系統S，它可以約化（reduce）為第二個系統S’，並且如果S和S’都是從代數曲線C和C’中產生的，那麼在曲線上的點的變換羣之間可建立代數對應；只考慮C中的一個點對應C’中的一個點，而C’中的一個點對應n個C中的點的情況。這樣就存在着某些屬於C的可還原積分，其週期表（the table of periods / Periodentabelle）有一個簡單的標準形式（normal form）。

兩個阿貝爾積分的例子所對應的週期表（摘自原書第36頁）。

此外，如已證明的，數n等於一個相關的θ函數的階（order）。現在我們知道，有某個富克斯函數可以單值化任何代數曲線，包括C’。曲線C’的基本多邊形可以被圓弧界定，而C中的每個這樣的多邊形都可由C’中的n個同樣的多邊形形成。積分和多邊形之間的相互關係產生了許多關於曲線C和C’的幾何事實，以及關於常負曲率空間中的共軛（congruent）多邊形的結論。有幾個例子給出了關於C和C’的美妙定理，它們可以用這種方式獲得。

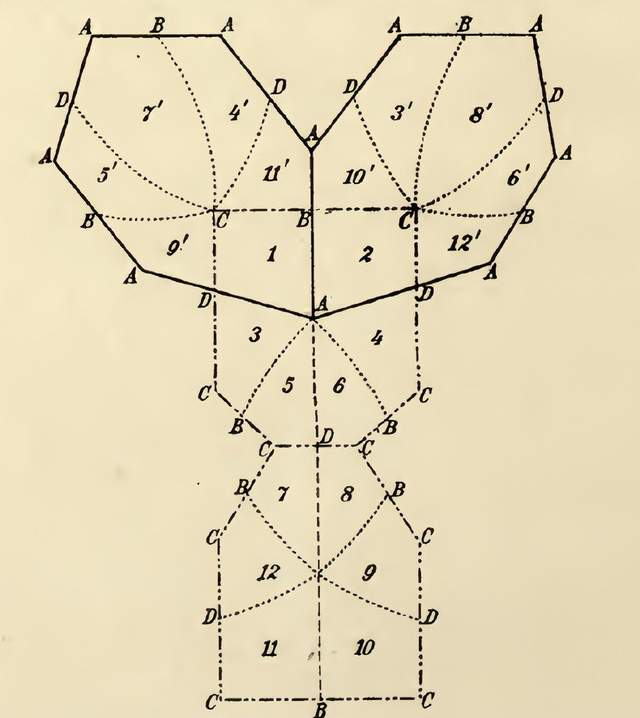
對一個例子（p=2, q=1, n=2）的富克斯羣，龐加萊對其所對應的基本域進行的圖示説明（摘自原書第40頁）。

5

超限數

這篇演講闡述了龐加萊對這一有爭議的數學領域中的一些微妙之處的態度。他堅持的主要觀點有兩個：第一，沒有任何數學實體不能用有限個詞來定義；第二，所有定義都必須是他所謂的“謂詞性的”（predicative）。例如，龐加萊反對人們熟悉的證明，即每個代數方程f(x)=0都有一個根，這個根取決於|f(x)|的最小值是否存在。因為從他的觀點來看，若要談論f(x)的所有的值，就必須涉及“用有限數量的詞定義的x的值”，而這並不可行，因為“可定義的x值的總和”這一概念是非謂詞性的。所涉及的困難在於，這個“總體”（totality）中存在着一些元素，而這些元素本身又是用“總體”來定義的，因此這個概念中出現了一個惡性循環。但演講中對“謂詞”一詞含義的闡釋並不清楚。

龐加萊首先考慮了理查德（Jules Richard）關於連續統（continuum）可數（denumerable）的證明（基於上述的第一個觀點）與康托爾關於連續統不可數的證據之間的明顯矛盾，但事實證明，這種矛盾並不存在，因為理查德採用了非謂詞性的定義。

他接着討論瞭如何從其立場出發重述代數方程根存在性的證明。結論中簡要提及了其他幾個問題。伯恩斯坦（Bernstein）定理對龐加萊來説是正確的，而連續統（在康托爾意義上）的良序問題對他來説似乎毫無意義。此外，他不確定第二個超限基數是否存在[6]。這些結論與其兩個主要觀點完全一致。

對龐加萊（以及許多其他數學家）的這些觀點，可能提出的主要反對意見是出於實用角度的，因為它們過於嚴格地限制了類（class）的概念。然而，這些質疑主要是出於直覺，而非邏輯能力。根據過去的經驗，這一事實表明了所提出觀點的合理性；它們是消除數學中無限性的一步，而我們不禁懷疑，無限類作為客觀存在的概念，在嚴格數學中是否會發揮任何重要的作用。

6

新力學

在這場閉幕的科普演講中，龐加萊探討了物理學的最新進展可能對力學產生變革。如果最終的運動方程是電磁場方程，而且實驗似乎也表明了這一點，那麼就會得出一系列令人震驚的結論：所有物體的速度都小於光速，而且它們的慣性（inertia）隨着速度的增加而增加；我們不可能通過任何實驗來判斷一個人是處於靜止狀態，還是相對於以太處於平移的勻速運動狀態；我們也不能説兩個事件在絕對意義上是同時發生的；更有甚者，所有物體都會在其運動方向上發生縮短。龐加萊正是研究了這個引人入勝的課題，尤其是其中所藴含的對力學的修正。

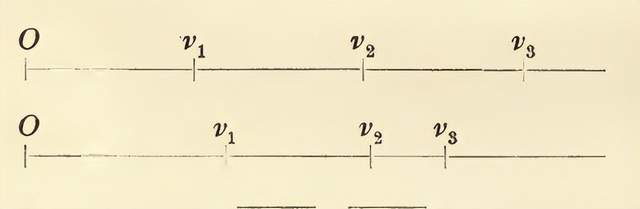
龐加萊對牛頓力學（上面線段）和新力學（下面線段）中的速度疊加的對比分析示意圖（摘自原書第52頁）。

只有在速度非常快的物體中，人們才有希望發現牛頓力學定律的偏差。水星的運動速度是所有行星中最快的，而恰恰是水星具有一種尚未得到解釋的微小反常現象。正如洛倫茲（H. Lorentz，1853-1928）所證明的那樣，新力學解釋了其中的一部分，而在其他任何地方，新力學都不會對行星的運動產生明顯的改變[7]。在介紹了這些事實之後，龐加萊總結道，牛頓力學將永遠是相對於光速而言速度很小的力學，因此將繼續保持其基本的重要性。

譯後記

希爾伯特和龐加萊是上世紀最偉大的數學家，也堪稱歷史上最偉大的數學家之二。他們都深刻影響了現代數學的發展，但二者的數學風格和對數學基礎的看法差異很大。希爾伯特以清晰的論述風格和形式主義立場而聞名，強調公理化方法，這也直接反映到他為20世紀數學發展指明道路的《數學問題》（Hilbert’s Problems）上。而龐加萊則更加側重於直覺，善於洞察問題的本質，常常通過非嚴格化的推理開闢新領域[他甚至因此被導師埃爾米特（Charles Hermite，1822-1901）和同門皮卡（Émile Picard，1856-1941）所批評]。因此就研究風格而論，希爾伯特有着德國式的嚴謹，龐加萊則富於法國式的浪漫。

這兩位數學家雖然研究興趣重疊不大，風格更加迥異，卻有着幾次重要的交往。在1908年夏，希爾伯特陷入抑鬱症，隨後在療養和治療中得到好轉，並證明了華林定理。同年，閔可夫斯基（Hermann Minkowski，1864-1909）正在研究電子的運動，著名的“閔可夫斯基時空”也受到了龐加萊引力理論的啓發，但二者在定性理解方面有本質差異。他們二人本有機會於當年春天在羅馬舉行的國際數學家大會（ICM）上和洛倫茲討論相對論，但因為龐加萊患病而錯過了機會。在1908年秋，希爾伯特寫信邀請龐加萊參加首屆沃爾夫斯凱爾講座（Wolfskehl Lectures）。沃爾夫斯凱爾（Paul Wolfskehl，1856–1906）原本是一名醫生，後師從庫默爾（Ernst Kummer，1810-1893）學習數學。他在1905年設立遺囑，“以10萬馬克獎勵第一個證明費馬大定理的人”，後於1906年去世，獎金為沃爾夫斯凱爾基金會運營，並資助了同名講座。而最終該獎在1997年授予懷爾斯（Andrew Wiles，1953-）。

龐加萊接受了邀請；他起初只計劃就兩個主題做演講，即弗雷德霍姆方法的應用和阿貝爾積分的約化。而在講座籌備過程中，閔可夫斯基因為突發闌尾炎而去世，年僅45歲。對希爾伯特而言，閔可夫斯基亦師亦友，二人感情十分深厚，因此他的離世對希爾伯特造成了巨大的晴天霹靂（Schlag aus dem heitersten Himmel）般的打擊，而龐加萊與閔可夫斯基的進一步合作也隨之化為泡影。但哥廷根的其他學者仍對龐加萊的電子理論感興趣，因此希爾伯特隨即要求龐加萊在演講中增加兩個主題，其一可以是關於理論物理學和天文學的，其二則可以帶有“邏輯哲學色彩”（Logisch-philosophischer Färbung）。龐加萊的答覆是，關於弗雷德霍姆方程的報告已經包含了理論物理學和天文學的主題——前者如赫茲波，後者如潮汐理論——但他同意增加一個從理查德悖論出發的邏輯哲學講座。

另外在世紀之交，由於電子在磁場中的偏轉（塞曼效應）、磁光學、電動體的電動力學和黑體輻射等重大問題不斷取得新發現，巴黎和哥廷根的理論學者紛紛轉入研究電子理論。龐加萊也在此領域做出了不少貢獻。可能是出於捍衞自己的時空和電子理論和促進交流的目的，龐加萊又在講座系列中增加了第六個關於新力學的講座，這就形成了該講座的最後計劃。而講座進行的1909年，正值克萊因（Felix Klein，1849-1925）的60壽辰。

講座的主要內容如下。前三次是關於弗雷德霍姆方程的理論和應用。1888年，杜布瓦-雷蒙（Paul Du Bois-Reymond，1831-1889）命名了“積分方程”，隨後弗雷德霍姆（Erik Ivar Fredholm，1866-1927）在1899-1903年左右就此發表了一系列研究論文，而希爾伯特在1904年看到弗雷德霍姆方程可以發展出解決邊值問題的新方法，後來這導向了希爾伯特空間的概念。龐加萊在此講座中首先回顧了弗雷德霍姆方程的基礎理論，隨後聯繫到其他數學家（包括希爾伯特）的關於無窮多個線性方程的理論。

第二次講座中，龐加萊首先使用球極投影將地球表面投影到平面上，而海岸線則被視為垂直的崖壁。此時，可以用二階偏微分方程刻畫水的運動，龐加萊將此方程轉化為積分方程，並先後概述了三種方法：希爾伯特和皮卡的方法（使用格林函數）、凱洛格（Oliver Kellogg，1878-1932）的勢函數方法以及柯西的留數微積分方法。

第三次講座則是關於弗雷德霍姆方程應用於赫茲波和無線電報的研究，並特別關注瞭如何將無線電信號發送到大洋彼岸的現實問題。當時的聽眾包括赫茲波方面的頂尖專家亞伯拉罕（Max Abraham，1875-1922）和理論物理學教授索末菲（Arnold Sommerfield，1868-1951）。

第四次講演則是另一主題，是關於富克斯函數和阿貝爾積分的約化的，這個問題無疑與龐加萊的自守函數主題研究有關（可參見《19世紀末的數學高峯：龐加萊的自守函數研究》）。龐加萊首先將此問題限制在代數曲線情形，然後將視野從函數論轉換到幾何和拓撲上，並證明了一系列關於富克斯多邊形和代數曲線的“重要而優美的定理”。

第五次是以超限數為題目的講演，開啓講演的話題是“理查德悖論”：可定義的對象只能是可數集，但不可數集卻存在。龐加萊使用“謂詞定義”和“非謂詞定義”的差異解決了這個矛盾，並在之後的講演中堅持謂詞性定義，並因此反對連續統基數的存在性和策梅洛（Ernst Zermelo，1871-1953）的良序原理，這無疑反映了他的“直覺主義”立場。

第六次講演則是關於“新力學”的演講。與前五次講座不同，這次講座中沒有數學公式，所以龐加萊選擇了法語（母語）進行演講：在這種新力學中，沒有物體能比光速更快，並且質量也會隨着物體速度的增加而變大。並且，位於兩個不同地點的觀察者的時鐘也會有不同的時間，這些觀念很顯然是相對論的基礎。然而，龐加萊仍然保留了“以太”的存在性。

這些講座涉及的領域各異：從積分方程的理論和應用，到函數論、阿貝爾積分和拓撲學的聯繫，再到數學基礎和超限數，最後涉及數學物理、相對論和時空的本質。由此可見龐加萊廣闊的視野和全面的數學才能。當然，這些內容也只是龐加萊研究的一小部分。

這次講座活動後來也發揮了它的歷史作用——它反映了當時的一些重要的數學論題，並促進了學者之間的交流和後續的研究。弗雷德霍姆方程的研究後來被希爾伯特等人發揚，導向積分方程的希爾伯特空間理論；赫茲波傳播方面的研究後來被索末菲注意到，並開展了相關研究；而“邏輯哲學”和“新力學”講座，無疑以數學基礎的討論和相對論為其後繼——它們都是極為廣闊深遠的領域，不僅重塑了人類的數學與時空觀念，更為未來技術發展開闢了無限可能。

因此，雖然已過去一個多世紀之久，但對我們而言，回顧世紀之交的這次系列講座，仍將是極富趣味的。而“數學史上最後一位通才”龐加萊和“大衞王”希爾伯特的這次交流活動，也成為了現代數學史和德法文化交流史中的一段佳話。

關於此講演更多的歷史和數學材料，可參閲：

Jeremy Gray, Henri Poincaré: A scientific biography.

Scott A. Walter, Poincaré-Week in Göttingen, in light of the Hilbert-Poincaré correspondence of 1908–1909, Mathematical Correspondences and Critical Editions，pp 297–310.

註釋

[1] 第一個演講: 關於弗雷德霍姆方程的一些評論（Remarques diverses sur l’équation de Fredholm，Acta Mathematica, vol. 33 (1909), pp. 57-86.）；第三個演講: 赫茲波的衍射（Sur la diffraction des ondes Hertziennes, Palermo Rendiconti, vol. 30 (1910), pp. 169-259）；第四個演講: 關於阿貝爾積分的約化和富克斯函數（Sur la réduction des intégrales Abéliennes et les fonctions Fuchsiennes, Palermo Rendiconti, vol. 29 (1909), pp. 281-336.) 第五個演講: 關於上述兩條筆記的思考（Réflexions sur les deux notes précédentes, Acta Mathematica, vol. 32 (1909), pp. 195-200.）和無限邏輯（La logique de l’infini, Revue de Metaphysique et de Morale, 1909, pp. 461-482.）

[2] 譯者注：前五次演講使用了德語。見Reinhard Kahle, “Poincaré in Göttingen”，選入“Poincaré, Philosopher of Science”一書，第87頁。

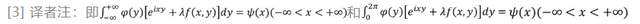
[4] 譯者注：赫茲波（Hertzian wave），無線電波的最初名稱。因赫茲在1888年發現電磁波，並證實了麥克斯韋（方程）關於電磁波存在的預言而得名。後多被用於指稱由電流振盪所產生的、波長較長（不小於1毫米）的電磁波。

[5] 在演講的最後指出，由於其中的重要項被忽略了，最終的結論需要修改。

[6] 譯者注：此處龐加萊指的是ℵ1。

[7] Newcomb 和 Seeliger 已經證明，水星和其他內行星運動中的異常在很大程度上可以通過分佈在太陽周圍的物質的引力來解釋，這些物質具有合理的質量，並且其分佈方式能夠產生已知的黃道光（zodiacal light）現象。

本文譯自G. D. Birkhoff, Poincaré’s Gottingen Lectures, Bull. Amer. Math. Soc. 17 (1911), 190-194.https://doi.org/10.1090/S0002-9904-1911-02017-1

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。

版權説明：歡迎個人轉發，任何形式的媒體或機構未經授權，不得轉載和摘編。轉載授權請在「返樸」微信公眾號內聯繫後台。