數學分岔與物理相變：不同領域的平行敍事與統一_風聞

從鐵磁體失磁到氣液相變，物理學揭示了自然界中“秩序突變”的普適規律；而在數學中，分岔與突變理論則以動力系統的語言描述穩定結構的更替。本文梳理了相變、分岔與臨界現象的統一框架，展示了它們如何在隨機動力系統中匯合為理解複雜系統“臨界點”的通用理論，為研究生態、氣候及社會系統的突變提供了系統科學基礎。

撰文 | 邱仲普

審核 | 樊京芳

在物理學中，從十九世紀末居里發現鐵磁體在特定温度下會突然失去磁性起，人們開始意識到自然界存在“秩序的突變”。隨後外斯的平均場理論給出第一個成功的宏觀描述，卻忽略了臨界點附近劇烈的漲落。楞次與伊辛通過自旋模型將磁性理解為有序與無序的競爭，但真正揭開相變本質的，是昂薩格在1944年對二維伊辛模型的嚴格求解，第一次以數學精度展示了連續相變的臨界行為。楊振寧在1951年完成了自發磁化的解析推導，使理論閉環，又與李政道提出“李–楊相變定理”，將配分函數零點引入複平面，把相變轉化為可解析的數學結構。隨着理論的發展，相變研究從經驗和近似走向嚴格與普適，催生了標度律、普適類與重整化羣理論，成為理解複雜系統與臨界現象的核心框架。

當物理學家們在物質狀態的迷宮中探索時，數學家們也在繪製一幅平行的地圖：他們處理的不是水或磁鐵，而是方程與幾何形態，卻關心同樣的問題——當一個系統受到外部緩慢驅動時，它的穩定性如何變化，哪些平衡點會消失，哪些新的穩定態會出現。他們以動力系統為語言，其研究核心是結構穩定性。

數學的敍事：分岔、突變與結構穩定性

想象一個在碗底靜止的小球。無論你如何輕微地推它，它最終都會回到碗底。這個系統是“結構穩定”的。現在，想象你慢慢地、持續地改變碗的形狀，讓它從U形變為M形。在某個瞬間，碗底中央的穩定點會消失，分裂成一個不穩定的高點和兩個新的穩定點。小球會突然滾向其中一個新的低谷。

這個從U到M的轉變，便是數學家所説的分岔：當系統參數連續變化時，其定性行為（如平衡點的數量和穩定性）發生突變的現象。這聽起來與統計物理中的相變何其相似！而數學的嚴謹之處在於，它為這些“突變”提供了詳盡的分類。

最基礎的分岔是鞍-結點分岔，在一個動力系統中（如圖1A），我們會看到隨着參數 r 的增大，系統的穩定平衡點和不穩定平衡點會相遇並消失，過程如圖1B、C所示。

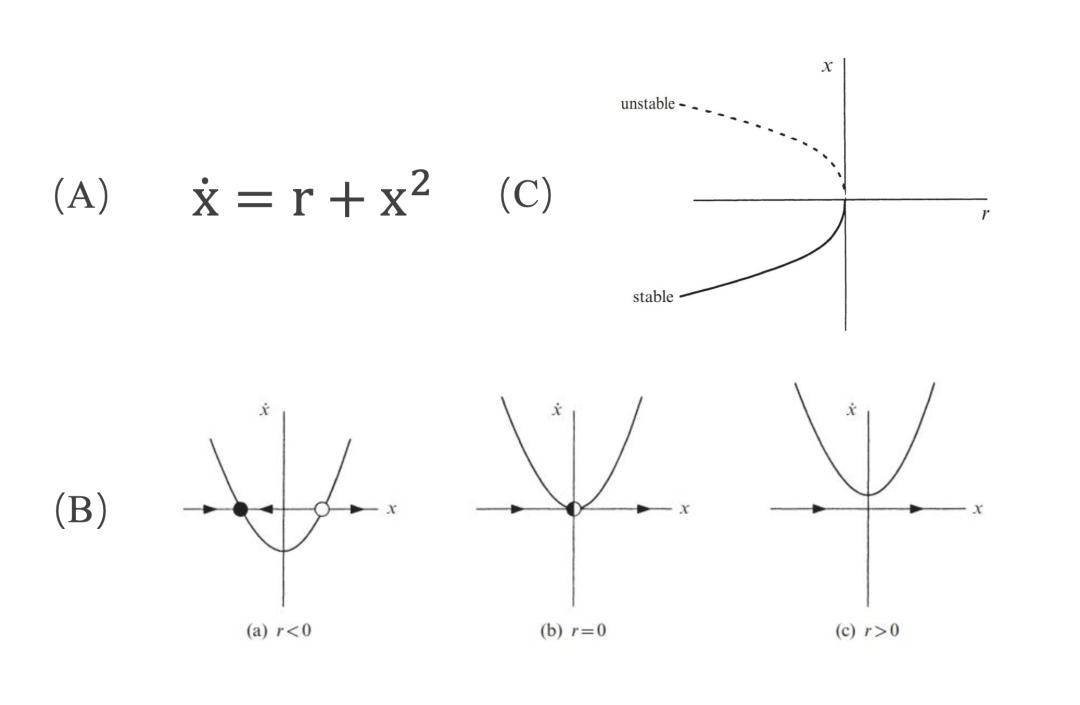圖1：鞍-結點分岔示意圖，（A）動力系統的典型微分方程形式，（B）r 變化時分岔的向量場，黑色實心點代表穩定平衡點，空心點代表不穩定平衡點，（C）分岔圖

更復雜的是跨臨界分岔，它不產生或消滅平衡點，而是讓兩個已有的平衡點在相遇時交換穩定性。最富戲劇性的是叉形分岔，它常見於具有對稱性的系統。它又分為兩種截然不同的類型，超臨界叉形分岔：當參數越過臨界點，中央的穩定態失穩，系統發生對稱性破缺，會平滑地、選擇性地進入兩側兩個新的穩定態之一。在臨界點附近，系統恢復力會變得極弱，出現臨界慢化現象。亞臨界叉形分岔：這則是一個陷阱。在中央穩定態失穩前，兩側早已潛伏着不穩定的分支。一旦越過臨界點，系統不會進入新的穩定態，而是會“爆炸”式地逃離，發生有限時間逃逸，其後果往往是災難性的。如圖2所示。

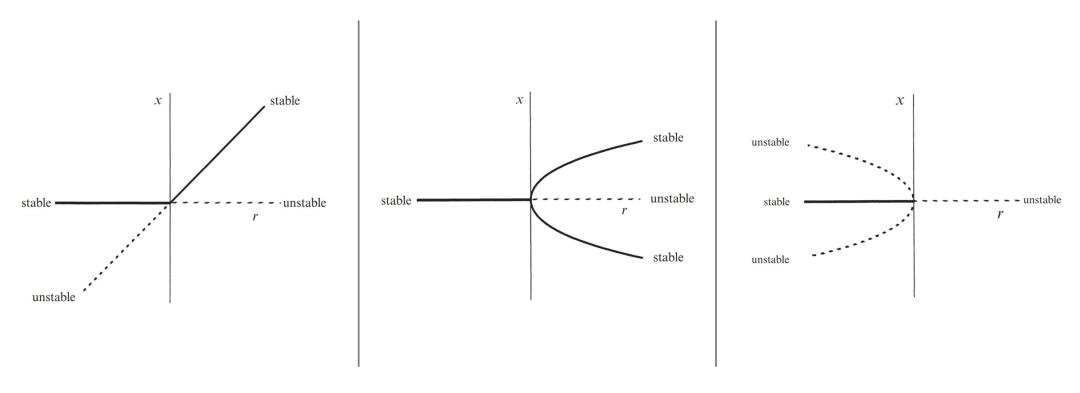圖2：從左到右，依次為跨臨界分岔圖，超臨界叉形分岔圖，亞臨界叉形分岔圖。

然而，現實世界比這些單參數模型更復雜。如果系統由兩個參數控制（即系統的餘維數為2），我們會觀察到更奇異的行為，比如尖點分岔，如圖3所示，這個動力系統的狀態在某一區域折成上下兩層，從側面看（投影）就出現分叉曲線。當外部條件（如圖中的h）慢慢變化、狀態點沿上層走到折邊盡頭時，它會突然跳到下層，此時就會出現滯後分叉；但如果是固定h，而調節r的話，則會出現我們剛才提到的超臨界叉型分叉。尖點分叉很好地將兩種不同的分叉統一在一個圖像當中，可以用來建模更復雜的突變行為。

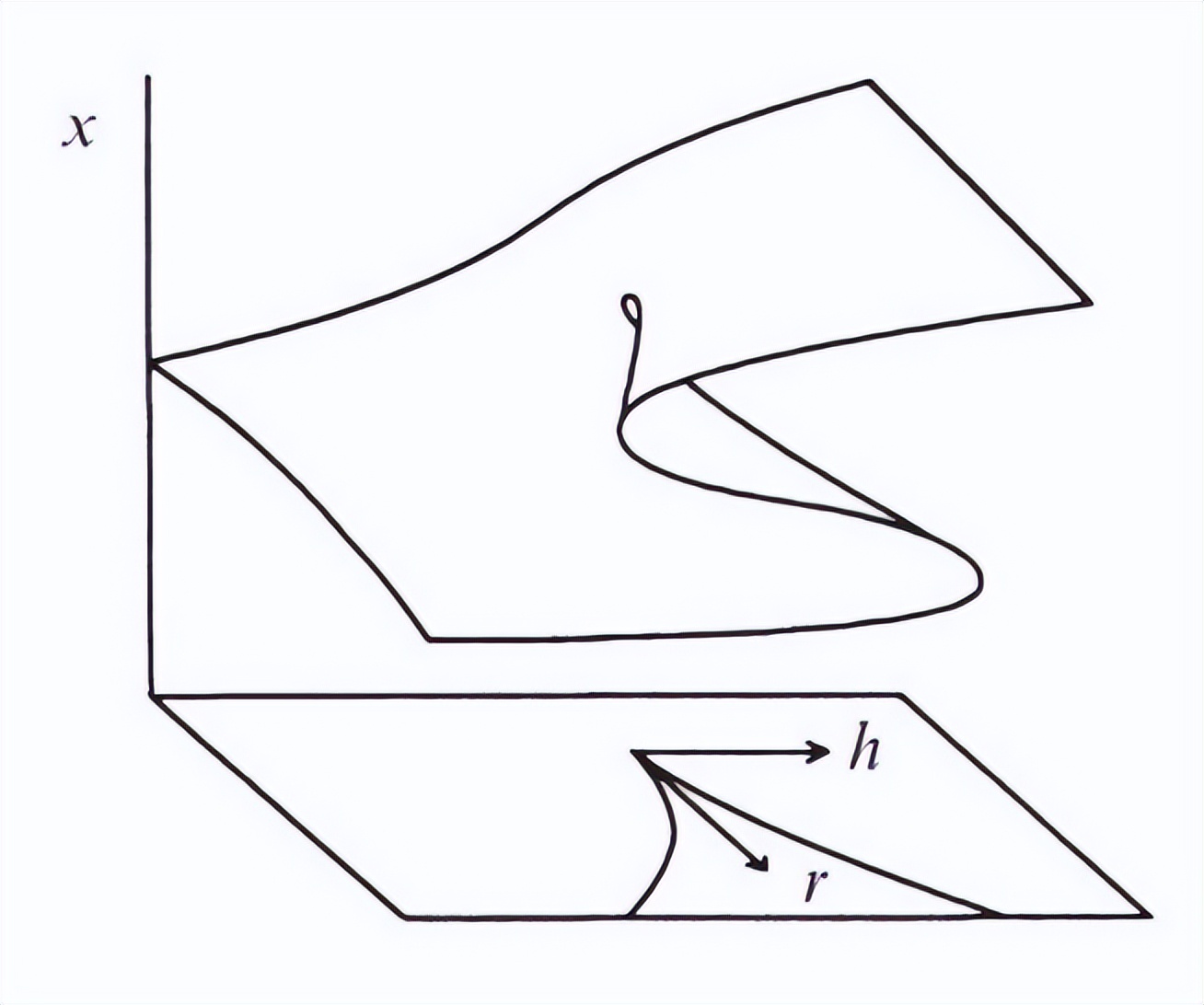圖3：尖點分岔示意圖

而聯繫物理系統，尖點分岔能很好地幫助我們理解物理學中鐵磁系統與氣液系統的性質：將如圖3所示的尖點分岔的三維摺疊向三個平面投影，獲得的結構和氣液系統與伊辛鐵磁體系統的相圖驚人地如出一轍（如圖4所示）。而楊振寧先生與李政道先生關於磁性格氣的工作，恰好在鐵磁系統和氣液系統之間架起了一座數學的橋樑，嚴格證明了二者的等價性。這讓我們意識到我們在鐵磁系統和氣液系統中觀察到的相變行為，其背後的數學結構來自於突變理論。

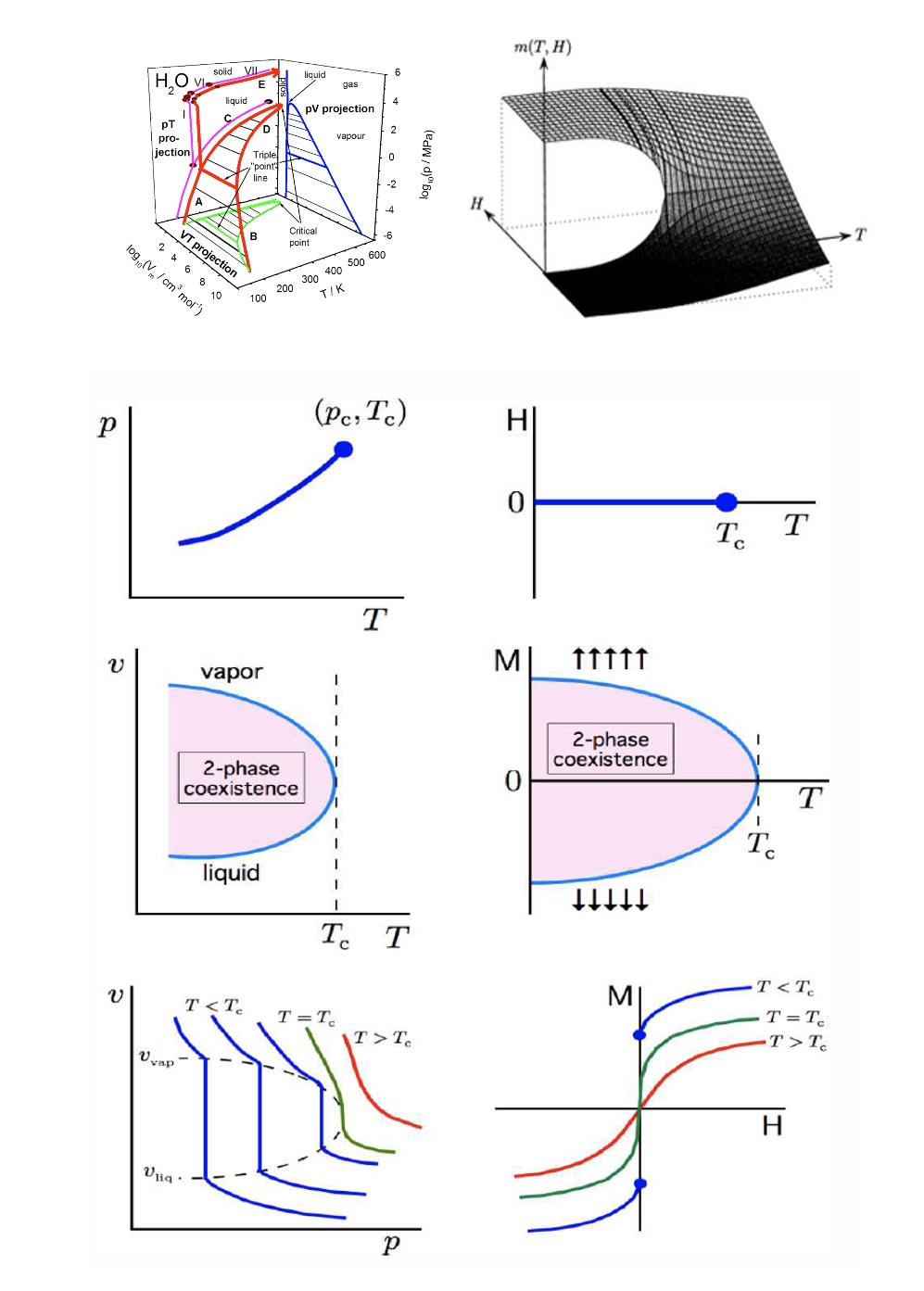圖4：左邊為氣液相圖，右邊為伊辛鐵磁體相圖，最上面兩個圖分別為水的三維相圖和 Ising模型的三維相圖，下面六個圖為三維相圖在不同面上的投影

法國數學家、菲爾茲獎得主勒內·託姆在20世紀60-70年代創立“突變論”（新三論之一），是分岔理論的自然發展。他將目光投向了所有這類光滑、連續的參數變化導致的分岔，並證明，當控制參數（餘維數）不多於四個時，所有可能的“突變”類型只有七種基本類型，即七種初等突變，如圖5所示。我們最初討論的鞍-結點分岔，是餘維數為1的突變；而尖點分岔，是餘維數為2的突變。此外，還有燕尾、蝴蝶、橢圓臍點等充滿詩意的名字，它們共同構成了數學家為自然界一切“突然的斷裂”所繪製的終極地圖。

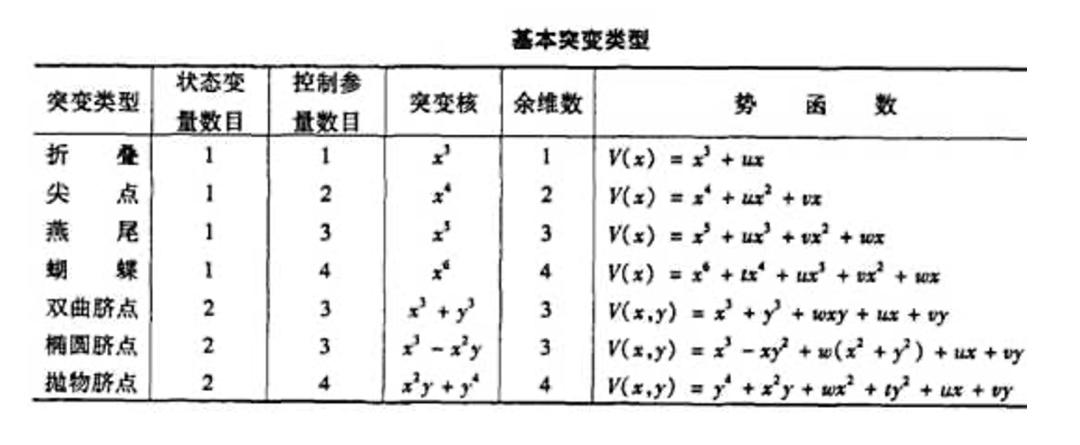圖5：七種基本突變的分類，展示其對應的維數、餘維數和勢函數

從數學上看，分岔理論為相變臨界現象提供了嚴謹的拓撲學和動力學基礎。它告訴我們，系統在臨界點附近的行為遵循着由系統內在結構決定的特定分岔模式，其類型由系統狀態變量的維數和控制參數的維數共同主導。物理學的相變和數學的分岔，如同兩條從不同源頭出發的河流，此刻正奔向同一個交匯的海洋。

統一的語言：從相變、分岔到臨界點

那麼，物理學的相變（和臨界）與數學的分岔（和突變）的統一描述是怎樣的？分岔是確定性動力系統的結構穩定性問題，而統計物理中的熱力學相變，可以看作是一類隨機動力系統的結構穩定性問題。

經典的平衡態統計物理處理的，正是包含億萬個粒子的系統。這種巨大的自由度，使得我們無法精確追蹤每個粒子，只能用概率和統計來描述。這本質上就是一種隨機動力系統——在平衡態的框架下，我們發展出了氣體動力學、近獨立子系統計等理論，特別是針對可以寫出哈密頓量的系統，19世紀末20世紀初，科學家建立系綜理論，在這一框架下，我們可以直接考察平衡態系統的相空間中的狀態分佈。但如果我們考察這樣的系統對應的非平衡動力學，比如寫出對應哈密頓量的過阻尼朗之萬方程，我們便馬上會意識到這就是一個含有噪聲的隨機動力系統。因此，正如平衡態統計物理只是在處理一類隨機動力系統的統計性質，相變與分岔在精神內核上也是統一的，都是關注於動力系統相空間的不變集的拓撲結構的變化。

這個統一的視角，為我們理解複雜系統中的臨界點（tipping point，見注1）提供了強大的理論武器。然而，真實的複雜系統中，如社會、生態和氣候系統等，存在着多種多樣的臨界點，其噪聲形式、分岔類型遠比上一節確定系統的分類更為豐富和微妙。那麼我們能否給出一個更廣泛的框架，用於統一描述這些臨界點呢？

注1：臨界在不同語境下，具有不同的含義。在熱力學和統計物理的語境下，Critical transition，翻譯為臨界相變。在一般的複雜系統中，Tipping point，翻譯為臨界點，它的含義更廣，可以考察非平衡系統的結構穩定性問題。

近年來，科學家們正努力建立一個更普適的理論框架，將Bifurcation-induced-tipping（分岔誘導突變）、Noise-induced-tipping（噪聲誘導突變）和Rate-induced-tipping（速率誘導突變）等不同類型的突變統一在同一個語言體系下。這個框架的核心思想，是關注系統內部存在的多個參數的對應時間尺度的相對性，這也是託姆的突變論的自然推廣。我們考慮這樣的一個隨機動力系統，如圖6所示：

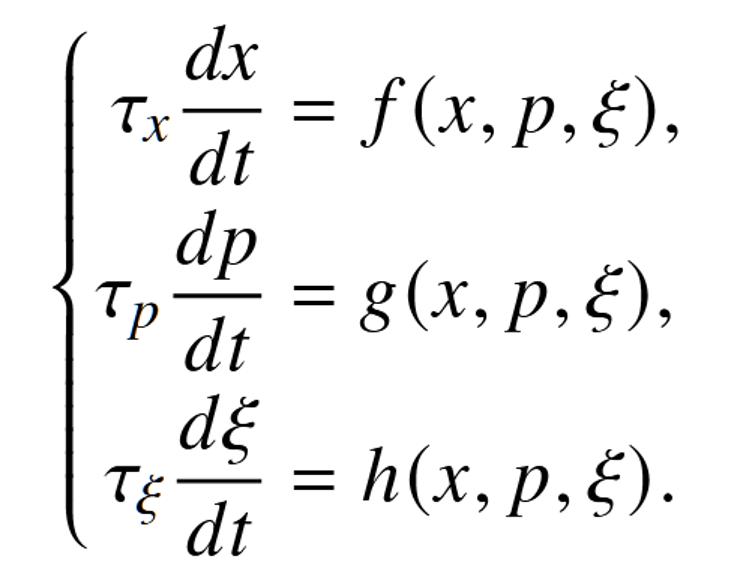圖6：隨機動力系統。來源： 馬智欽，預測非線性隨機系統的臨界轉變: 模型和數據驅動方法研究

化；而噪聲變化又如此之快，其影響在統計意義上被平均掉了。此時，我們的動力系統就優雅地退回到經典的分岔和突變理論，可以按照維度n和餘維度m進行像勒內·託姆那樣的分類。這正是B型臨界（B-tipping）。

因此，通過分析這三個時間尺度的相對關係，我們可以找到更多更符合實際的臨界類型：

續的隨機噪聲將使系統逐漸偏離平衡區。此時，中等強度的隨機噪聲 ξ 就可能成為“臨門一腳”，觸發tipping的發生。甚至，系統會在新舊狀態附近“閃爍”（flickering），頻繁地在兩個狀態之間跳躍。例如在洱海等生態系統中觀察到，它在“草型清水穩態”和“藻型濁水穩態”兩種狀態間轉換。

數 p 的變化速度太快，系統內部的動態過程 x 根本來不及跟上參數的變化系統，因而未能追蹤連續變化的吸引子。即使最終的參數值 p 本身位於一個穩定的區域內，系統也可能因為“追不上”而崩潰。例如典型的堆肥炸彈模型，在西伯利亞泥炭/永凍土區，若大氣升温的速率過快，土壤呼吸迅速增強並放熱，進一步升高土温，形成“升温→呼吸增強→再升温”的正反饋；系統“追不上”移動的穩定態，突然躍遷至高温高排放態，出現土壤温度失控上衝與大規模碳釋放的“堆肥炸彈”不穩定性。

物理學把“相變”從經驗觀察推進為可計算的問題，分岔與突變理論用動力系統的語言描述穩定狀態如何更替。兩條路線共同指向“結構與穩定性的變化”，構成了一個既能證明、也能分類的框架。通過這樣的統一定義和分類，我們就更加深刻地理解了不同類型臨界之間的關係，這為我們關注具體某個系統中的臨界現象打下了堅實的理論基礎。

本文經授權轉載自微信公眾號“集智俱樂部”。

作者：邱仲普 北京師範大學系統科學學院在讀博士

審核：樊京芳 北京師範大學系統科學學院教授、院長

出品：中國科協科普部

監製：中國科學技術出版社有限公司、北京中科星河文化傳媒有限公司

特 別 提 示

1. 進入『返樸』微信公眾號底部菜單“精品專欄“，可查閲不同主題系列科普文章。

2. 『返樸』提供按月檢索文章功能。關注公眾號，回覆四位數組成的年份+月份，如“1903”，可獲取2019年3月的文章索引，以此類推。