轉學術論文|看陳平如何扒下弗裏希(分享第一個諾經獎的人)經濟理論的數學底褲_風聞
末那识-学以养识,以识统学。(心迷法华转,心悟转法华)2019-04-19 10:19
按:筆者在前文“電動汽車崛起完美演繹了代謝增長論!兼談扒下若干諾獎經濟學理論的數學底褲”中提到的陳平扒下了弗裏希經濟理論的數學底褲而讓我們清楚看明白了所謂諾獎理論究竟是個什麼(金金玉其外敗絮其中)料子,但只是照錄了故事。幸好找到了陳平的學術論文,其中有詳細的數學證明。本文也是也是從PDF倒騰過來的(不能直接從PDF用軟件轉換成word),可費了牛勁了,請大家珍惜。另,版面原因,原文中的腳註此處省略了。
經濟週期理論的弗裏希模型之謎:
均衡經濟學和永動機模型
The Mystery of Frisch Model in
Business Cycle Theory:
Equilibrium Economics and
Perpetual Motion Machine
陳平
1999年5月原稿,2015年6月18日中文修訂稿
《清華政治經濟學報》2015年6月(將出版)
摘要
1969年分享第一個諾貝爾經濟學獎的弗裏希,以噪聲驅動週期模 型主導了宏觀經濟學和計量經濟學的發展。實際上,弗裏希在1933年 非正式會議上構想的模型,早在1930~1945年間就被物理學的研究所 否定,文章也從未在計量經濟學期刊上正式發表。奇怪的是,弗裏希 本人從1934年起就對該模型保持沉默,連他的諾獎演説也不置一詞。 用弗裏希模型分析美國實際GDP數據,也得不到持續的經濟週期。破 解弗裏希模型之謎,可以看清經濟週期理論中週期外生論和內生論的 爭論,關係到經濟學界均衡論和演化論的不同視角。非線性動力學的 最新成果告訴我們,只有非線性振子才能產生持續的經濟週期,也就 是熊彼特提出的生物鐘。
Abstract
Ragnar Frisch shared the First Nobel Prize in 1969. The Frisch model of noise-driven cycles had dominating influence in macro and econometrics since 1930s. In fact, the Frisch model was announced in an informal conference in 1933, but never formally published in Econometrica. Frisch model was also rejected by physicists in 1930 to 1945. Strangely, Frisch kept silence to his model since 1934 and did not mention a word to his award-winning model. We analyzed the US real GDP data by means of the Frisch model, which failed to produce persistent cycles in US economy.
Cracking the Frisch mystery around the Frisch model reveals the conflicting thoughts between the exogenous and endogenous school in business cycle theory, and between equilibrium and evolutionary paradigm. The latest advancement in nonlinear dynamics tells us that only nonlinear oscillator is capable of generating persistent cycles that is the Schumpeter’s insight on biological clock in business cycle theory.
關鍵詞:經濟週期,噪聲驅動,弗裏希模型,永動機,阻尼振盪
Keywords: business cycles, noise-driven, Frisch model, perpetual motion machine, damped oscillation
科學的悲劇是:醜陋的事實扼殺了美麗的假説。
托馬斯·H·赫胥黎(英國演化生物學家,1870)
視而不見比瞎子還瞎。
喬納森·斯威夫特(愛爾蘭作家, 1667-1745)
一 引言:弗裏希模型的歷史之謎
經濟週期理論中的一個焦點問題是持續經濟週期的性質和起源。宏觀和計 量經濟學界主要有兩派理論思維:經濟週期的內生學派和外生學派(Zarnowitz, 1992)。熊彼特將經濟週期看作經濟有機體的生命律動(Schumpeter, 1939)。 古德温引入非線性和混沌振子來描述持續經濟週期(Goodwin, 1951、1990)。 然而,經濟混沌的早期證據沒有引起主流經濟學的重視,因為經濟混沌的存在 意味着對經濟學的均衡理論和參數計量經濟學的數學基礎的嚴重挑戰(Barnett and Chen 1988, Chen 1988 、 1993 、 1996a 、 1996b ; Brock and Sayers1988)。與此相反,自20世紀30年代以來,外生學派統治了主流經濟學;創始 人是拉格納弗裏希(Kydland,1995)。
哈耶剋意識到,經濟週期的經驗主義特點很難用均衡理論來理解(Hayek, 1933)。 弗裏希指出噪聲驅動阻尼振子可以解釋市場穩定和持續週期(Frisch 1933年)。他在一篇非正式的會議論文中宣傳了他的猜想,但是沒有給出數學證明。弗裏希模型對物理學家並不新奇,因為諧振子和布朗運動的相互作用已經 研究過了。與弗裏希的信念相反,物理學家們從1930年以來就知道布朗運動影 響下的諧振子不能產生持續振動(Uhlenbeck and Ornstein,1930;Wang and Uhlenbeck,1945)。
今天弗裏希的信念仍然被主流經濟學家和計量經濟學家所接受。這在科學 史上是一件咄咄怪事,因為弗裏希從未發表他承諾的論文,他的猜測早被物理 學家的工作否定。第一屆諾貝爾經濟學獎竟然頒給一個從未正式發表,而且被 科學實驗證明是錯誤的永動機模型,這在經濟學思想史上是值得研究的一大謎 團。重新檢討弗裏希模型,將有助於我們理解自由主義經濟學的均衡思維是如 何數理化的。自穩定市場均衡模型的源頭是外來噪聲模型,而非內生週期模 型。主流宏觀經濟學研究經濟週期理論的名家,從弗裏希噪聲驅動模型開始, 加上盧卡斯的微觀基礎論、薩金特的理性預期檢驗、季德蘭和普萊斯哥特的真 實經濟週期學派(RBC),共四次獲得諾貝爾經濟學獎;再加上伯南克的金融加速 器模型,都是弗裏希模型的變種 (Lucas, 1972;Sargent and Wallace, 1975; Kydland and Prescott,1982;Bernanke et al,1996)。至今美聯儲 和歐洲央行指導經濟政策的計算機模型,都是噪聲驅動的計量模型。他們只是 把弗裏希模型的微分方程簡化為差分方程組,把弗裏希的一個噪聲源,增加到 盧卡斯的三個噪聲源,以至伯南克的幾十個噪聲源。他們企圖用噪聲驅動模型 4 來説明市場經濟是自身穩定的,造成市場波動以至經濟危機的源頭只是外來隨 機噪聲的衝擊,以此證明政府政策干預的效果有限。
為何經濟學界在長達60年的時間裏忽視布朗運動研究的基本理論,至今堅 持噪聲驅動持續週期的錯誤信念,這是研究經濟學思想史的一大歷史謎團。 我 們從小就會盪鞦韆。鞦韆是最常見的阻尼振盪,空氣摩擦力會使初始起擺的秋 千逐漸停擺。要讓鞦韆維持擺盪,必須有人不時推動鞦韆來克服摩擦力。請問 大家:推鞦韆的方式是按照鞦韆擺盪的頻率來推,還是胡亂推,才能使鞦韆繼續擺盪?小孩都知道推鞦韆當然要有節奏地推。即使不懂物理學或熱力學,任 何有常識的人都不難看出阻尼諧波週期不能通過外部的隨機衝擊來維持。每次 我問物理學家和經濟學家同樣的問題,物理學家都異口同聲地否定噪聲驅動周 期的可能性。只有經濟學家被集體洗腦到失去常識的程度,即使有數理背景的 經濟學家也大多被我問的不知所措。至今沒有幾個主流經濟學家敢直面我對弗 裏希模型的批評。
本文原為討論稿發表於1999年(Chen,1999),投給西方主流經濟學期刊被 拒絕發表。我們只能通過國際會議的邀請報告和筆者的文集向經濟學家證明弗 裏希模型的謬誤(Chen,2005、2008、2010)。在2009年金融危機之後,我們用 中文重新發表,是啓發年青的經濟學人,不要盲目崇拜獲得諾貝爾經濟學獎的 理論。據我們三十多年用物理學方法分析經濟學數據和模型的經驗基礎,統治 主流宏觀計量經濟學的是以弗裏希為代表的對自由市場的信念,而非實踐檢驗 過的科學知識。金融危機之後,全世界的經濟學人都在呼喚經濟學的新思維。 我們就從弗裏希模型的歷史教訓開始。
在這篇論文中,我們首先給出弗裏希模型的簡短歷史,然後討論它的數學 理論和實證內涵。我們説明經濟週期的線性決定論模型有參數空間機制不穩定 5 性的缺陷。外部噪聲對線性振子的影響可以通過朗之萬方程和福克-普朗克方程 來研究。我們可以獲得諧振子在布朗運動下的解析解。振幅和自相關函數的指 數衰減表明噪聲驅動不可能產生持續的週期振盪。我們可以用美國實際GDP(國 內生產總值)的數據來估計諧振子的固有頻率和摩擦係數。最後,我們討論諧 振子布朗運動模型的主要啓示,和經濟週期理論線性模型的基本問題。只有非 線性的振子模型可以解釋觀察到的持續週期振盪(Chen,1988)。它的經濟學含 義就是熊彼特把經濟週期比喻為生物鐘(Schumpeter,1939)。哈耶克ᨀ出的內 生自發秩序和物理學家普里戈金提出的自組織系統是複雜科學在經濟學應用的哲學基礎(Hayek,1991;Nicolis and Prigogine,1977)。
二 有關弗裏希噪聲驅動經濟週期模型的歷史文獻
從20世紀30年代開始,弗裏希經濟週期模型一直主導宏觀經濟學的經濟周 期理論。1933年的一篇非正式會議報告中,弗裏希提出,可以用阻尼振子來描述市場經濟的自身穩定性,而持續經濟週期的存在可以由外來的持續衝擊維持 (Frisch 1933),這就是他的噪聲驅動週期模型的核心思想。他説(標出重點 的斜體字由筆者所加):
“當一個經濟系統產生振盪時,這些振盪經常會衰減。但在現實中,我們 觀察到的週期通常沒有衰減。如何解釋維持波動的持續機制呢?
我認為特別富有前景的方法,是研究一個決定論動力系統暴露於一連串紊亂的衝擊之下,使衝擊得以不斷改變系統的時間演化, 這種機制可以引入必需 的能量來維持系統的波動……
我將討論這些問題。詳細的數學分析,讀者可以參閲《Econometrica(計量 經濟學)》期刊即將發表的論文。”
作為物理學家,我馬上意識到弗裏希構想的實質是單熱源的熱力學第二類 永動機,它企圖將環境波動的隨機熱能轉化為動能做機械功,以克服摩擦力來 維持振盪。弗裏希構想違反了熱力學第二定律。有高中物理知識的學生都知道 這是不可能實現的。
弗裏希在討論阻尼振子的傳播問題和噪聲影響的脈衝問題之後宣稱:
“我們關注平均週期和平均振幅是合理的。換言之,這能給出實際統計觀 察中得到的曲線類型。我這裏暫不給出任何嚴格的證明,它將和大量的數據模擬一起,即將發表在前面提到的《計量經濟學》期刊最新的論文中。”
我們查閲了《計量經濟學》期刊,在“近期論文預告”的欄目中三次出現 弗裏希論文的標題:
拉格納·弗裏希:“從線性算子和隨機衝擊的視角研究變化諧波”。
弗裏希的論文預告刊登在《計量經濟學》期刊的第一卷,包括第2期(1933 年4月)第234頁、第3期(1933年7月)第336頁、還有第4期(1933年10月)。 奇怪的是,從第二卷第1期開始(1934年1月),這一預告消失得無影無蹤。弗裏希承諾的論文從來沒有出現過。這一怪事出現的原因不難理解:因為弗裏希 本人是這一新創的計量經濟學學會旗艦期刊的主編。只有他能決定發表或撤下 已經公告的論文。
36年之後,弗裏希因為在經濟週期理論方面的工作而獲得第一屆諾貝爾經 濟學獎。1969年10月,埃裏克·倫德伯格教授代表瑞典皇家科學院做了如下陳述 (斜體字由筆者添加)(Lundberg 1969):
“……弗裏希教授在(20世紀)30年代早期的開創性工作涉及週期理論的 動態模型。他給出貨幣約束下投資和消費支出的微分方程,會產生波長為四年 和八年的阻尼振盪。如果讓系統經受隨機衝擊,他證明這些不均勻的波動得以持續,和現實的觀察非常接近。弗裏希構造的數學模型走在時代前面,他吸引了許多後繼者。他對統計假設檢驗方法的貢獻也是如此。”
在他1970年6月於斯德哥爾摩發表的諾貝爾經濟學獎獲獎演説中,弗裏希大談鍊金術到粒子物理學的故事,但是隻字未ᨀ他獲獎的經濟週期模型(Frisch 1981)。我們從以上史實可以推測,弗裏希早從1934年起就悄悄放棄了他的模型。我猜弗裏希從1934年起應當熟知隨機過程的成果,因為他的出身是應用數 學家。但是弗裏希從未公開承認他猜想的錯誤,只是令人奇怪地避而不談自己的最高成就。
倫德伯格宣稱“弗裏希走在時代前面”,他的歷史知識不足。事實上,物理學家在1930年就解決了布朗運動影響下的諧振子問題,並在40年代對證明做 了改進(Uhlenbeck and Ornstein,1930;Chandrasekhar,1943;Wang and Uhlenbeck,1945),其中錢德拉色卡還是獲得諾貝爾獎的物理學家。 隨機過程的經典論文出過文集,有關布朗運動的成果數學家們早已熟知(Wax 1954), 是筆者當物理學研究生修統計力學課程時熟知的參考文獻。這些物理學家用不 同方法的研究得出同樣的結論,布朗運動不能維持衰減的諧波振盪。1963年以 來對決定性混沌的發現進一步表明,只有內生的非線性振子才能產生持續的經濟週期(Chen,1988;Goodwin,1990;Hao 1990)。
三 線性確定性週期模型在參數空間的機制不穩定性
弗裏希非常清楚線性週期的侷限(Goodwin,1993)。眾所周知,簡諧波的 週期波動可以通過一個二階線性微分方程或差分方程產生。只有當摩擦係數為 零時,週期波動才能持續存在。任何參數空間的係數偏差可能將諧波的週期振 蕩轉變為阻尼振盪或爆炸振盪。這種現象在數學模型中被稱為參數空間的邊際 穩定,或機制不穩定性(regime instability)。
(一)離散時間(DT)的薩繆爾森模型
線性週期的一個典型例子是薩繆爾森的乘數-加速數模型(Samuelson 1939)。早期版本的薩繆爾森模型用的是離散時間(discrete time) 的差分方程。

其中,0 <a<1 , b>0,C是消費;I是投資;E是政府支出;Y是收入。 我們得到一個二階差分方程:
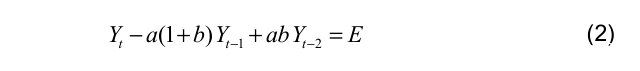
它的解是:
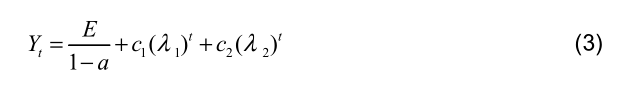
其中λ1和λ2是特徵方程的兩個根

它的判別式是:

當 ∆ < 0 時我們有振盪解。
週期解的條件是
ab = 1 (6b)
出於經濟意義考慮,我們必須有:
0<a<1,b> 0 (6c)
方程(6a、b、c)組成了方程解主要機制(regime)的邊界。模型有四種類 型的解:(1)阻尼振盪機制 DO;(2)爆炸振盪機制 EO;(3)單調收斂機制 MC;(4)單調遞增機制 MI。週期振盪只能出現於阻尼振盪機制DO和爆炸振盪 機制EO之間的邊界線上。參數改變越界時,解的機制發生突變,例如從阻尼振 蕩變為爆炸振盪。圖1中給出了參數空間的機制分佈圖。可見,週期振盪機制 PO只具備參數空間的邊際穩定或週期振盪的機制不穩定。些微的參數變化就可 能使週期解不存在。這是當年弗裏希反對線性決定論週期模型的理由 (Goodwin,1993)。
問題是線性隨機過程的單位根(unit-root)模型和協整(co-integration)模型具 有同樣的機制不穩定性(Nelson and Plosser,1982;Engle and Granger, 1987)。線性隨機過程的根在單位圓內穩定,單位圓外不穩定,只在單位圓上只 有邊際穩定性。只有非線性動力學系統才能克服線性系統週期解或隨機衝擊解 的機制不穩定性問題(Chen,2005)。
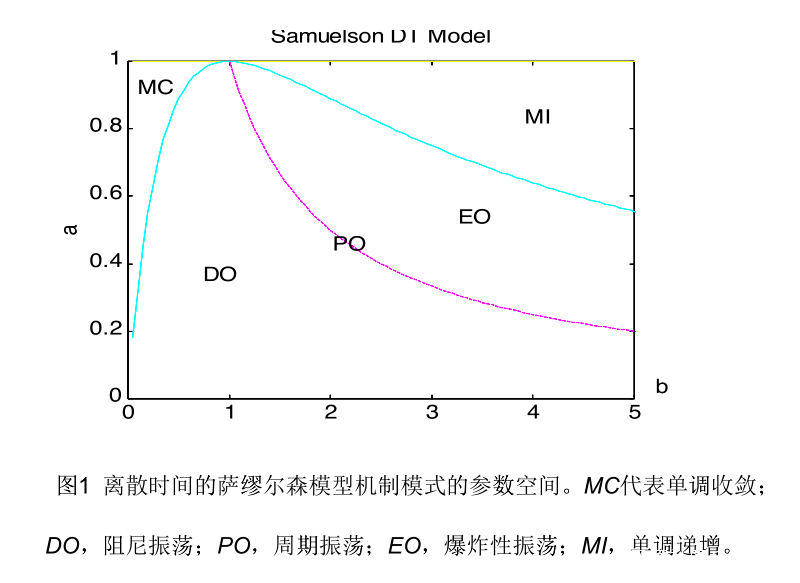
圖1 離散時間的薩繆爾森模型機制模式的參數空間。MC代表單調收斂;
DO,阻尼振盪;PO,週期振盪;EO,爆炸性振盪;MI,單調遞增。
(二) 連續時間(CT)的薩繆爾森模型
經濟學家也研究過經濟週期連續時間(continuous time)的微分方程模型 (Scarfe,1977)。我們這裏只討論上述薩繆爾森模型的連續時間版本,以理 解離散時間和連續時間線性模型之間的關係。在薩繆爾森模型中,我們簡單地 用導數代替差分。我們可以得到:

我們得到一個二階微分方程
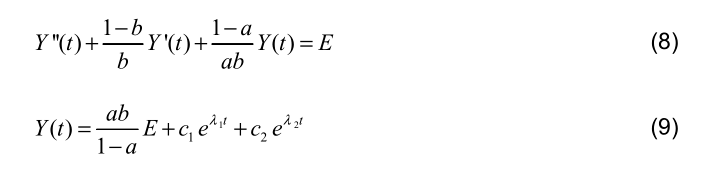
其中λ1 和λ2 是特徵方程(10)的兩個根。

當λ1=λ2 =λ 時,我們得到

只有當 b=1 時我們才得到週期解。類似地,這一連續時間模型也有4個動 態機制。它的參數空間的機制分佈如 圖2 所示。與離散時間(DT)的薩繆爾 森模型相比,唯一的區別就是週期性邊界位置的改變。週期振盪在參數空間中 仍然只有邊際穩定性。
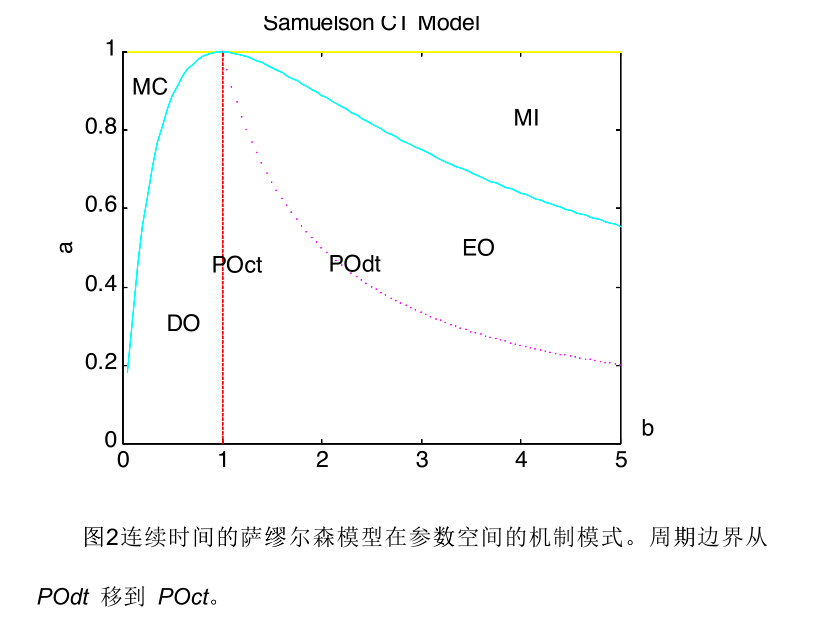
圖2連續時間的薩繆爾森模型在參數空間的機制模式。週期邊界從 POdt 移到 POct。
四 諧振子的布朗運動模型
經濟學中的弗裏希模型,在物理學中叫做諧振子的布朗運動模型。在弗裏 希1933年的論文中,他只是以如下方程的形式討論了阻尼振子,但是沒有給出解析解。

弗裏希知道,當摩擦係數κ不為0的時候,這一方程式將產生角頻率為ω的 衰減振盪。如果加入一系列的隨機衝擊,弗裏希模型就變成一個諧波振子的布 朗運動,這是自由粒子布朗運動的一個自然擴展。問題在於,是否布朗運動可 以維持諧振子的持續振盪。
愛因斯坦於1905年解答了關於自由粒子的布朗運動理論(Einstein 1926)。諧波約束粒子的布朗運動理論於1930年得到解答,並於20世紀40年 12 代改進了數學證明(Uhlenbeck and Ornstein, 1930;Chandrasekhar, 1943; Wang and Uhlenbeck, 1945)。他們的主要發現是,在自由粒子的隨機衝擊 下,諧波粒子將產生阻尼諧振。我們引入朗之萬方程來描述這個問題。
諧波粒子的運動可以通過以下方程式來描述:

此處 x(t)是座標, dx(t)/dt是粒子的速度,Ξ(t)是具有零均值且以σ為標準差的連續時間的高斯白噪聲,Γ 是擴散係數,κ 是摩擦係數。
朗之萬方程可以轉換成福克-普朗克方程:
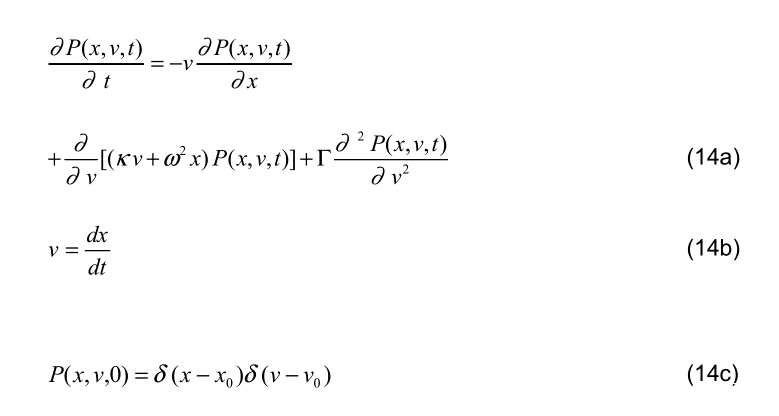
可以用傅里葉變換的方法求解這一方程。我們計算它的平均位移和相關係數如下:

若角頻率ω和頻率 f 的關係為ω = 2πf ,則固有角頻率ω可以通過特徵方程求得。對於布朗運動衝擊下的的角頻率ω1,我們可以得到:

我們可以計算簡諧粒子的均方位移和相關係數(Wang and Uhlenbeck, 1945)。
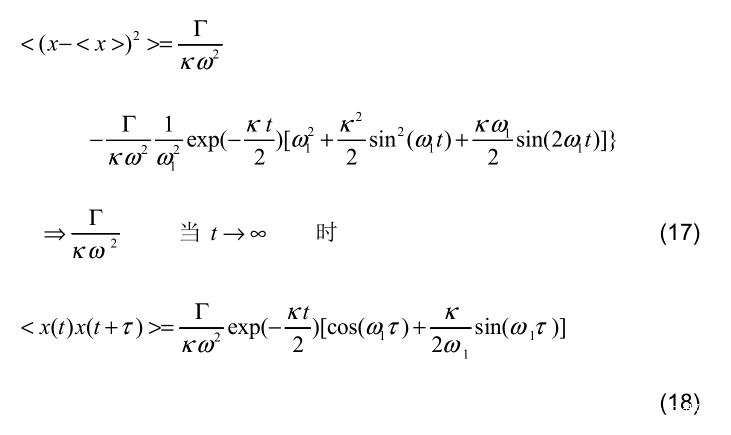
此處τ是時滯。
從式(18)可見,布朗運動下諧振子的位移趨於一個常數,而描述簡諧周 期振盪的相關係數隨時間指數衰減到零,最後只有剩餘的隨機擾動,觀察不到 週期振盪。
愛因斯坦給出的自由粒子的布朗運動具有不同的結果,自由粒子的漂移隨時間增加,這是典型的擴散過程(Einstein 1926)。

方程(17)和(18)的正確性已經過物理實驗的檢驗(Barnes and Silverman,1934)。我們確認,布朗運動影響下的諧振子沒有帶來擴散過程, 它的振盪將快速衰減成殘餘波動,最終沒有可觀察的持續週期振盪。
五 諧振子布朗運動模型對美國經濟週期數據的應用
布朗運動下阻尼振盪的主要特徵可以通過它的自相關函數來估計(Wang and Uhlenbeck 1945):
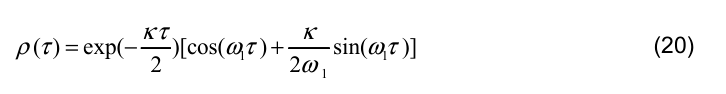
位移的自相關函數表現出以指數衰減的振盪。我們可以將振幅衰減到初始值的( 1/e ~ 0.368倍)的弛豫時間定義為Tκ

我們可以看到,所求得的振盪頻率是由自由振盪的固有頻率和摩擦係數決 定的。我們可以通過經驗數據的自相關函數來直接估計κ 和 ω1。噪聲驅動的 阻尼振子僅形成短暫的週期T1。實現週期 T1 的時間尺度與弛豫時間Tκ相似。可以通過自相關函數的第一個零值點 Tac 對所求得的諧振頻率 f1 進行估計。
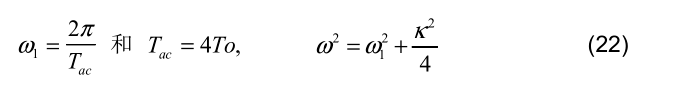
由於自相關函數只對平穩過程有定義,我們必須選擇一種合適的方法消解經驗時間序列的增長趨勢,把非平穩時間序列變換為平穩時間序列。趨勢消解 方法的選擇亦等價於觀察參照系的選擇(Chen,1996a、1996b)。經濟計量 分析中的一階差分(FD)趨勢消解法意味着最小的時間窗和白化濾波器。對數 線性(LD)趨勢消解法的時間窗最大,覆蓋整個歷史週期。HP濾波器確定了 一個具有中等時間窗的非線性的平滑趨勢。(Hodrick and Prescott,1997; Kydland and Prescott,1982)
我們將剩餘方差和噪聲方差的比率定義為增益係數G:

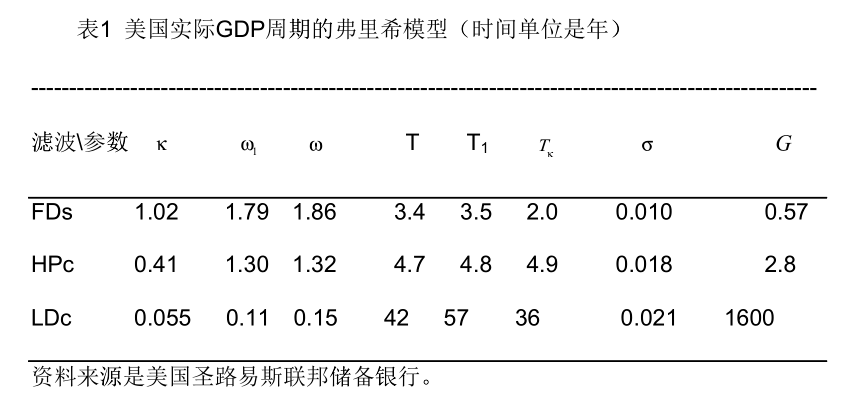
用美國實際GDP的季度數據(1947-1992),我們得到的結果見表1。因為 實際GDP季度數據的自相關函數在僅僅一個或兩個週期內迅速衰減,所以估計 的誤差相當大。然而這些參數的數量級仍然處於可接受的合理範圍內。通過表1 可以觀察到一些定量特徵。
表1 美國實際GDP週期的弗裏希模型(時間單位是年)
資料來源是美國聖路易斯聯邦儲備銀行。
這裏, κ 摩擦係數,ω1是求得的角頻率,ω是固有角頻率,T1= 2π/ ω1 是觀察到的週期,T = 2π/ω 是固有周期,Tκ是弛豫時間,σ 是標準差,G是增益係數。
由表1可見,布朗運動衝擊下的諧振子將迅速地在一個到兩個週期內停止簡 諧振盪,時間尺度從2到40年不等,取決於所選擇的經濟週期的觀察參照系。 一階差分(FD)趨勢消解法的弛豫時間Tκ最短的,只有2年。對數線性趨勢消 解法(LD)的弛豫時間最長,達36年。HP濾波器得到的弛豫時間和國家經濟研究 局(NBER)定義的一個經濟週期的平均長度差不多,為4.9年。顯然,隨機衝擊 並不能維持阻尼振子的持續性經濟週期。
同時,不同的時間窗顯示不同的經濟週期圖形。一階差分(FD)序列的方 差最小且週期最短,只有3.5年。而對數線性(LD)週期的最大,週期長達57 年。HP週期的方差和週期介於兩者之間。其中,只有一階差分(FD) 消除法對 外部噪聲有阻尼作用,HP和對數線性消解法均對外部噪聲具有放大作用。這些 特徵表明HP參照系相對FD和LD來説,比較接近經濟學界定義的經濟週期的度量。
綜上所述,均衡經濟學的理論框架不能為經驗分析ᨀ供理論自洽的分析方 法。新古典的宏觀增長理論隱含着經濟增長的線性對數LD趨勢(索洛 1956)。由於對數線性趨勢的決定取決於起點和終點的邊界依賴,等價於經濟觀察的路徑依賴。 弗裏德曼是均衡視角的倡導者,他更青睞和歷史無關的FD 差分法(1969)。由於FD是把有色(即有周期信號)時間序列漂白化的功能,一階差分消解法被廣泛應用於計量經濟學和金融分析,以支持均衡理論的預 言。從表1可見,FD差分消解法的問題是更難識別經濟週期的外部驅動源,因 17 為外部驅動源的波動幅度必須比美國經濟的波動幅度還要大。目前世界上不存 在比美國還大的實體經濟可以製造對美國的隨機衝擊。
六 結論
弗裏希的經濟週期模型不能解釋市場經濟中觀察到的持續週期振盪。由於 熱力學第二定律的制約,布朗運動或隨機衝擊不能傳送足夠的能量去克服摩擦 力來維持週期振盪。計量經濟學自創生起一直對噪聲模型᧿寫經濟波動情有獨鍾,從斯盧茨基開始做數值模擬(Slutsky 1937)到弗裏希建立噪聲驅動週期 模型,他們着迷的是經濟序列表面的紊亂無序。由於時代的限制,他們沒有想 到經濟波動的不規則週期其實和生命的生物鐘相似。持續經濟週期的非線性特 性在經濟學界遲遲不被承認,噪聲驅動經濟週期主導主流經濟學的錯誤信念要 負主要的歷史責任。
話説回來,弗裏希推測確實了提出科學上饒有趣味的問題,尤其是外部噪 聲對決定性振子的影響。依據非線性動力學的知識,我們所知持續週期只由非 線性動力系統產生。例如範德波爾模型的極限環解產生的是振幅均勻的週期振 蕩,這在經濟數據中從未被發現(Van der Pol 1926)。振幅不規則而頻帶有限 的色混沌和觀察到的經濟週期比較接近(Rössler,1976;Chen,1988、 1996a)。當噪聲值超過Ḁ臨界值時,外部噪聲可以改變非線性振子的穩定機制 (Chen,1987b)。
諾貝爾經濟學獎怎麼會授予給從未發表而且錯誤的弗裏希猜測,這在科學 史上是一個前所未有的謎團。科學史的學者可能對歷史細節更感興趣,例如為 何弗裏希放棄了他許諾發表的論文,為何從1934年起他對自己的得意模型保持 沉默,連諾獎演説也不置一詞。我們更感興趣對比物理學和經濟學的不同文 18 化。在伽利略和愛因斯坦以後的時代,指導物理學家研究的不是哲學信念,而 是觀察實驗。似乎經濟學界還處在哥白尼以前的時代,主流經濟學家對自由市 場的信仰,超過對科學研究的好奇和對經驗事實的尊重。當然,西方經濟學家不缺有識之士。牛津大學的著名計量經濟學家亨得理(David Hendry)早在1980 年就提出一個發人深思的問題:計量經濟學究竟是科學還是鍊金術(Hendry, 1980、2001)? 主持聖塔菲研究所經濟研究和組織索羅斯基金會經濟學新思維的著名經濟學家, 紐約新學院大學教授伏裏(Duncan Foley),對亞當·斯密創立的西方主流經濟學的評價是“理論神學”(Foley, 2010)。他們的深度批評, 值得中國的經濟學家注意。和自然科學相比,經濟學只是未經實驗檢驗的前科學而已。經濟學真正的實驗科學化,還有待於我們這一代人的努力。
我們對比研究經濟週期的混沌模型和噪聲驅動模型的經驗,發現非線性和非均衡視角優越性,受阻於均衡經濟學的烏托邦學説,最典型的案例就是弗裏 希模型。弗裏希模型的空想特徵與熱力學歷史上的永動機非常相似。熊彼特認為經濟週期與心臟搏動相似,生物鐘的這一特徵是有機體的精髓(Schumpeter 1939)。根據非均衡熱力學,生物鐘只能出現於具有能量流、信息流和物質流 的耗散系統中(Prigogine 1980);因此,非均衡機制是經濟演化的本質,非 線性動力學則是經濟週期的根源。弗裏希謎團給我們上了有價值的一課,就是 經濟學家和其他學科的對話交流,將給跨學科研究創造累累碩果。
致謝
作者感謝與Victor Zarnowitz、David Kendrik、Linda Reichl、William Schieve、閆沐霖、何祚庥等學者的討論。作者也感謝駱穎浩對薩繆爾森連續時 19 間模型的研究,Julia Buxter對我英文草稿的編輯,以及符雲玲和王興華老師的中文翻譯。
本文是筆者在美國德克薩斯大學研究和中國北京大學執教的期間完成的。 非線性經濟動力學的跨學科研究是我在普里戈金統計力學與複雜系統中心用物 理學方法研究經濟問題的長期努力的成果。筆者感謝伊利亞• 普里高金教授的支持, 美國Welch基金會和IC2 研究院的資助。筆者也感謝北京大學中國經濟研究中心林毅夫教授對跨學科研究的同情和幫助。 當然,本文引發的爭議和可能 的錯誤概由筆者負責。
參考文獻
Barnes, R.B. and S. Silverman. 1934. Brownian Motion as a Natural Limit to all Measuring Processes, Review of Modern Physics, 6, 162- 192.
Barnett, W. A. and P. Chen (陳平). 1988. The Aggregation-Theoretic Monetary Aggregates Are Chaotic and Have Strange Attractors: An Econometric Application of Mathematical Chaos, in W. Barnett, E. Berndt, and H. White eds., Dynamic Econometric Modeling, Cambridge: Cambridge University Press, pp. 199-246.
Bernanke, B., M.Gertler, and S.Gilchrist,. 1996. The Financial Accelerator and Flight to Quality, Review of Economics and Statistics, 78, 1-15.
Brock, W. A. and C. Sayers, 1988. Is the Business Cycles Characterized by Deterministic Chaos?" Journal of Monetary Economics, 22, 71-80.
Chandrasekhar, S. 1943. Stochastic Problems in Physics and Astronomy, Reviews of Modern Physics, 15(1), 1-89.
Chen, P. (陳平) . 1987. Origin of the Division of Labor and a Stochastic Mechanism of Differentiation, European Journal of Operational Research, 30, 246-250.
Chen, P. (陳平) . 1988. Empirical and Theoretical Evidence of Monetary Chaos, System Dynamics Review, 4, 81-108.
Chen, P. (陳平). 1993. Searching for Economic Chaos: A Challenge to Econometric Practice and Nonlinear Tests, in R. Day and P. Chen eds. Nonlinear Dynamics and Evolutionary Economics, Oxford: Oxford University Press.
Chen, P. (陳平) . 1996a. Trends, Shocks, Persistent Cycles in Evolving Economy: Business Cycle Measurement in Time-Frequency Representation, in W. A. Barnett, A. P. Kirman, and M. Salmon eds., Nonlinear Dynamics and Economics, Chapter 13, pp. 307-331, Cambridge University Press.
Chen, P. (陳平). 1996b. A Random Walk or Color Chaos on the Stock Market? - Time-Frequency Analysis of S&P Indexes, Studies in Nonlinear Dynamics & Econometrics, 1(2), 87-103.
Chen, P. (陳平) . 1999. The Frisch Model of Business Cycles: A Spurious Doctrine, But a Mysterious Success,” CCER Working Paper, #E1999007, China Center for Economic Research, Peking University, Beijing, China; IC2 Working Paper 99-05-01, University of Texas at Austin, Austin, TX, USA.
Chen, P. (陳平 ). 2002. Microfoundations of Macroeconomic Fluctuations and the Laws of Probability Theory: the Principle of Large Numbers vs. Rational Expectations Arbitrage, Journal of Economic Behavior & Organization, 49, 327-344.
Chen, P. (陳平). 2005. Evolutionary Economic Dynamics: Persistent Business Cycles, Disruptive Technology, and the Trade-Off between Stability and Complexity, in Kurt Dopfer ed., The Evolutionary Foundations of Economics, Chapter 15, pp.472-505, Cambridge University Press, Cambridge.
Chen, P. (陳平). 2008. Equilibrium Illusion, Economic Complexity, and Evolutionary Foundation of Economic Analysis, Evolutionary and Institutional Economics Review, 5(1), 81-127.
Chen, Ping. (陳平) . 2010. Economic Complexity and Equilibrium Illusion: Essays on Market Instability and Macro Vitality, Chapter 13, London: Routledge.
Einstein, A. 1926. Investigations on the Theory of the Brownian Movement, edited by R. Fürth, Methuen, London.
Engle, R.F. and C.W.J.Granger. 1987. Co-Integration and Error Correction: representation, Estimation, and Testing, Econometrica, 55(2), 251-276.
Foley, Duncan K. 2008. Adam’s Fallacy: A Guide to Economic Theology, Harvard University Press.
Frisch, R. 1933. Propagation Problems and Impulse Problems in Dynamic Economics, in Economic Essays in Honour of Gustav Cassel, George Allen & Unwin, London.
Frisch, R. 1981. From Utopian Theory to Practical Applications: The Case of Econometrics, American Economic Review, 71(6), 1-16 (1981).
Goodwin, R. M. 1951. The Nonlinear Accelerator and the Persistence of Business Cycles," Econometrica, 19, 1-17.
Goodwin, R. M. 1990. Chaotic Economic Dynamics, Clarendon, Oxford.
Goodwin, R. M. 1993. My Erratic Progress toward Economic Dynamics: Remarks made at banquet, Tuesday, April 18, 1989, In R.H. Day and 21 P. Chen eds. Nonlinear Dynamics and Evolutionary Economics, Oxford University Press, Oxford.
Hao, B.L.(郝᷿林)1990. Chaos II, World Scientific, Singapore.
Hayek, F. A. 1933, 1966. Monetary Theory and the Trade Cycle, A.M. Kelley Publishers, New York.
Hayek, F.A. 1991. The Fatal Conceit: The Errors of Socialism. The University of Chicago Press.
Hendry, David F. 1980,2001. Econometrics: Alchemy or Science? Essays in Econometric Methodology, Oxford University Press, Oxford.
Hodrick, R. J. and E. C. Prescott. 1981. Post-War US. Business Cycles: An Empirical Investigation, Discussion Paper No. 451, Carnegie-Mellon University.
Kydland, F.E. 1995.Business Cycle Theory, Edward Elgar.
Kydland, F. E. and E. C. Prescott. 1982. Time to Build and Aggregate Fluctuations, Econometrica, 50(6), 1345-1370.
Lucas, R. E. Jr. 1972. Expectations and the Neutrality of Money, Journal of Economic Theory, 4(2), 103-124.
Nelson, C. R. and C. I. Plosser. 1982. Trends and Random Walks in Macroeconomic Time Series, Some Evidence and Implications, Journal of Monetary Economics, 10, 139-162.
Nicolis, G. and I. Prigogine. 1977. Self-Organization in Nonequilibrium Systems, Wiley, New York.
Prigogine, I. 1988. From Being to Becoming: Time and Complexity in the Physical Sciences, Freeman, San Francisco. 中譯本:普里戈金 著, 2007. 從存在到演化,北京大學出版社。
Rössler, O. E. 1976. An Equation for Continuous Chaos, Physics Letters A, 57, 397-398.
Sargent, Thomas & Wallace, Neil. 1975. ‘Rational’ Expectations, the Optimal Monetary Instrument, and the Optimal Money Supply Rule. Journal of Political Economy 83 (2): 241–254.
Scarfe, B. L. 1977. Cycles, Growth, and Inflation, McGraw-Hill, New York.
Schumpeter, J. A. 1939. Business Cycles, A Theoretical, Historical, and Statistical Analysis of the Capitalist Process, McGraw-Hill, New York.
Slutsky, E. E. 1937. The Summation of Random Causes as the Source of Cyclic Processes, Conjuncture Institute, Moscow (1927); Econometrica, 5, 105-146.
Solow, R. M. 1956. A Contribution to the Theory of Economic Growth, Quarterly Journal of Economics, 70(1), 65-94.
Uhlenbeck, G.E. and L.S.Ornstein. 1930. On the Theory of Brownian Motion, Physical Review, 36(3), 823-841.
Van der Pol, B. 1926. On Relaxation-Oscillations, The London, Edinburgh and Dublin Phil. Mag. & J. of Sci., 2(7), 978-992.
Wax, N. 1954. Selected Papers on Noise and Stochastic Processes, Dover, New York.
Wang, M. C. (王明貞) and G. E. Uhlenbeck. 1945. On the theory of the Brownian Motion II, Review of Modern Physics, 17(2&3), 323-342.
Zarnowitz, V. 1992. Business Cycles, Theory, History, Indicators, and Forecasting, pp. 196-198, University of Chicago Press, Chicago.